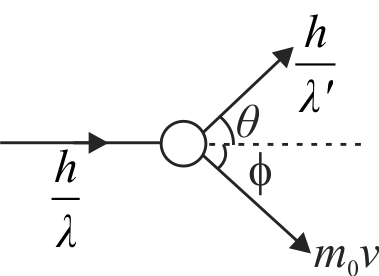
357887 A photon of wavelength \(\lambda\) is scattered from an electron, which was at rest. The wavelength shift \(\Delta \lambda\) is three times of \(\lambda\) and the angle of scattering \(\theta\) is \(60^{\circ}\). The angle at which the electron recoiled is \(\phi\). The value of \(\tan \phi\) is : (electron speed is much smaller than the speed of light)
357887 A photon of wavelength \(\lambda\) is scattered from an electron, which was at rest. The wavelength shift \(\Delta \lambda\) is three times of \(\lambda\) and the angle of scattering \(\theta\) is \(60^{\circ}\). The angle at which the electron recoiled is \(\phi\). The value of \(\tan \phi\) is : (electron speed is much smaller than the speed of light)
357887 A photon of wavelength \(\lambda\) is scattered from an electron, which was at rest. The wavelength shift \(\Delta \lambda\) is three times of \(\lambda\) and the angle of scattering \(\theta\) is \(60^{\circ}\). The angle at which the electron recoiled is \(\phi\). The value of \(\tan \phi\) is : (electron speed is much smaller than the speed of light)
357887 A photon of wavelength \(\lambda\) is scattered from an electron, which was at rest. The wavelength shift \(\Delta \lambda\) is three times of \(\lambda\) and the angle of scattering \(\theta\) is \(60^{\circ}\). The angle at which the electron recoiled is \(\phi\). The value of \(\tan \phi\) is : (electron speed is much smaller than the speed of light)