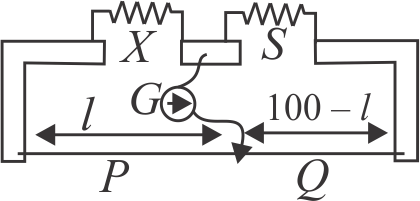357281
In a metre bridge experiment resistances are connected as shown in the figure. Initially resistance \(P = 4\Omega \) and the netural point \(N\) is at 60 \(cm\) from \(A\). Now an unknown resistance \(R\) is connected in series to \(P\) and the new position of the neutral point is at 80 \(cm\) from \(A\). The value of unknown resistance \(R\) is-
357282 The resistance per centimeter of a meter bridge wire is \(r\), with \(X \Omega\) resistance in left gap. Balancing length from left end is at \(40\,cm\) with \(25\,\Omega \) resistance in right gap. Now the wire is replaced by another wire of \(2\,r\) resistance per centimeter. The new balancing length for same will be at
357284
With a resistance of ‘\(X\)’ in the left gap and a resistance of \(9\Omega \) in the right gap of a meter bridge, the balance point is obtained at 40 \(cm\) from the left end.
In what way and to which resistance should a \(3\Omega \) resistance be connected to obtain the balance at 50 \(cm\) from the left end?
357285 Two resistances are connected in two gaps of a metre bridge. The balance point is 20 \(cm\) from the zero end. \(A\) resistance of 15 \(ohms\) is connected in series with the smaller of the two. The null point shifts to 40 \(cm\). The value of the smaller resistance in \(ohms\) is
357281
In a metre bridge experiment resistances are connected as shown in the figure. Initially resistance \(P = 4\Omega \) and the netural point \(N\) is at 60 \(cm\) from \(A\). Now an unknown resistance \(R\) is connected in series to \(P\) and the new position of the neutral point is at 80 \(cm\) from \(A\). The value of unknown resistance \(R\) is-
357282 The resistance per centimeter of a meter bridge wire is \(r\), with \(X \Omega\) resistance in left gap. Balancing length from left end is at \(40\,cm\) with \(25\,\Omega \) resistance in right gap. Now the wire is replaced by another wire of \(2\,r\) resistance per centimeter. The new balancing length for same will be at
357284
With a resistance of ‘\(X\)’ in the left gap and a resistance of \(9\Omega \) in the right gap of a meter bridge, the balance point is obtained at 40 \(cm\) from the left end.
In what way and to which resistance should a \(3\Omega \) resistance be connected to obtain the balance at 50 \(cm\) from the left end?
357285 Two resistances are connected in two gaps of a metre bridge. The balance point is 20 \(cm\) from the zero end. \(A\) resistance of 15 \(ohms\) is connected in series with the smaller of the two. The null point shifts to 40 \(cm\). The value of the smaller resistance in \(ohms\) is
357281
In a metre bridge experiment resistances are connected as shown in the figure. Initially resistance \(P = 4\Omega \) and the netural point \(N\) is at 60 \(cm\) from \(A\). Now an unknown resistance \(R\) is connected in series to \(P\) and the new position of the neutral point is at 80 \(cm\) from \(A\). The value of unknown resistance \(R\) is-
357282 The resistance per centimeter of a meter bridge wire is \(r\), with \(X \Omega\) resistance in left gap. Balancing length from left end is at \(40\,cm\) with \(25\,\Omega \) resistance in right gap. Now the wire is replaced by another wire of \(2\,r\) resistance per centimeter. The new balancing length for same will be at
357284
With a resistance of ‘\(X\)’ in the left gap and a resistance of \(9\Omega \) in the right gap of a meter bridge, the balance point is obtained at 40 \(cm\) from the left end.
In what way and to which resistance should a \(3\Omega \) resistance be connected to obtain the balance at 50 \(cm\) from the left end?
357285 Two resistances are connected in two gaps of a metre bridge. The balance point is 20 \(cm\) from the zero end. \(A\) resistance of 15 \(ohms\) is connected in series with the smaller of the two. The null point shifts to 40 \(cm\). The value of the smaller resistance in \(ohms\) is
357281
In a metre bridge experiment resistances are connected as shown in the figure. Initially resistance \(P = 4\Omega \) and the netural point \(N\) is at 60 \(cm\) from \(A\). Now an unknown resistance \(R\) is connected in series to \(P\) and the new position of the neutral point is at 80 \(cm\) from \(A\). The value of unknown resistance \(R\) is-
357282 The resistance per centimeter of a meter bridge wire is \(r\), with \(X \Omega\) resistance in left gap. Balancing length from left end is at \(40\,cm\) with \(25\,\Omega \) resistance in right gap. Now the wire is replaced by another wire of \(2\,r\) resistance per centimeter. The new balancing length for same will be at
357284
With a resistance of ‘\(X\)’ in the left gap and a resistance of \(9\Omega \) in the right gap of a meter bridge, the balance point is obtained at 40 \(cm\) from the left end.
In what way and to which resistance should a \(3\Omega \) resistance be connected to obtain the balance at 50 \(cm\) from the left end?
357285 Two resistances are connected in two gaps of a metre bridge. The balance point is 20 \(cm\) from the zero end. \(A\) resistance of 15 \(ohms\) is connected in series with the smaller of the two. The null point shifts to 40 \(cm\). The value of the smaller resistance in \(ohms\) is
357281
In a metre bridge experiment resistances are connected as shown in the figure. Initially resistance \(P = 4\Omega \) and the netural point \(N\) is at 60 \(cm\) from \(A\). Now an unknown resistance \(R\) is connected in series to \(P\) and the new position of the neutral point is at 80 \(cm\) from \(A\). The value of unknown resistance \(R\) is-
357282 The resistance per centimeter of a meter bridge wire is \(r\), with \(X \Omega\) resistance in left gap. Balancing length from left end is at \(40\,cm\) with \(25\,\Omega \) resistance in right gap. Now the wire is replaced by another wire of \(2\,r\) resistance per centimeter. The new balancing length for same will be at
357284
With a resistance of ‘\(X\)’ in the left gap and a resistance of \(9\Omega \) in the right gap of a meter bridge, the balance point is obtained at 40 \(cm\) from the left end.
In what way and to which resistance should a \(3\Omega \) resistance be connected to obtain the balance at 50 \(cm\) from the left end?
357285 Two resistances are connected in two gaps of a metre bridge. The balance point is 20 \(cm\) from the zero end. \(A\) resistance of 15 \(ohms\) is connected in series with the smaller of the two. The null point shifts to 40 \(cm\). The value of the smaller resistance in \(ohms\) is