357056
Wheatstone bridge principle is used to measure the specific resistance \(\left(S_{1}\right)\) of given wire,having length \(L\), radius \(r\). If \(X\) is the resistance of wire, then specific resistance is; \({S_1} = X\left( {\frac{{\pi {r^2}}}{L}} \right).\)
If the length of the wire gets doubled then the value of specific resistance will be:
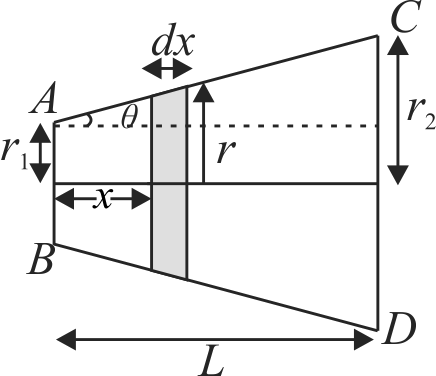
357059 A portion of length \(L\) is cut out of a conical solid wire. The two ends of this portion have circular cross-sections of \({r_1}\;\) and \({r_2}({r_1} > {r_2})\) radii. It is connected lengthwise to a circuit and a current \(I\) is flowing in it. The resistivity of the material of the wire \(\rho .\) Calculate the voltage developed across it.
357056
Wheatstone bridge principle is used to measure the specific resistance \(\left(S_{1}\right)\) of given wire,having length \(L\), radius \(r\). If \(X\) is the resistance of wire, then specific resistance is; \({S_1} = X\left( {\frac{{\pi {r^2}}}{L}} \right).\)
If the length of the wire gets doubled then the value of specific resistance will be:
357059 A portion of length \(L\) is cut out of a conical solid wire. The two ends of this portion have circular cross-sections of \({r_1}\;\) and \({r_2}({r_1} > {r_2})\) radii. It is connected lengthwise to a circuit and a current \(I\) is flowing in it. The resistivity of the material of the wire \(\rho .\) Calculate the voltage developed across it.
357056
Wheatstone bridge principle is used to measure the specific resistance \(\left(S_{1}\right)\) of given wire,having length \(L\), radius \(r\). If \(X\) is the resistance of wire, then specific resistance is; \({S_1} = X\left( {\frac{{\pi {r^2}}}{L}} \right).\)
If the length of the wire gets doubled then the value of specific resistance will be:
357059 A portion of length \(L\) is cut out of a conical solid wire. The two ends of this portion have circular cross-sections of \({r_1}\;\) and \({r_2}({r_1} > {r_2})\) radii. It is connected lengthwise to a circuit and a current \(I\) is flowing in it. The resistivity of the material of the wire \(\rho .\) Calculate the voltage developed across it.
357056
Wheatstone bridge principle is used to measure the specific resistance \(\left(S_{1}\right)\) of given wire,having length \(L\), radius \(r\). If \(X\) is the resistance of wire, then specific resistance is; \({S_1} = X\left( {\frac{{\pi {r^2}}}{L}} \right).\)
If the length of the wire gets doubled then the value of specific resistance will be:
357059 A portion of length \(L\) is cut out of a conical solid wire. The two ends of this portion have circular cross-sections of \({r_1}\;\) and \({r_2}({r_1} > {r_2})\) radii. It is connected lengthwise to a circuit and a current \(I\) is flowing in it. The resistivity of the material of the wire \(\rho .\) Calculate the voltage developed across it.