356515
Energy levels \(A,B\) and \(C\) of a certain atom correspond to increasing values of energy, i.e.,\({E_A} < {E_B} < {E_C}.\) If \({\lambda _1},{\lambda _2}\) and \({\lambda _3}\) are wavelength corresponding to transitions \(C\) to \(B,B\) to \(A\) and \(C\) to \(A\) respectively then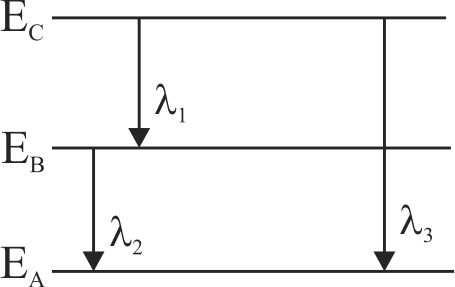
356515
Energy levels \(A,B\) and \(C\) of a certain atom correspond to increasing values of energy, i.e.,\({E_A} < {E_B} < {E_C}.\) If \({\lambda _1},{\lambda _2}\) and \({\lambda _3}\) are wavelength corresponding to transitions \(C\) to \(B,B\) to \(A\) and \(C\) to \(A\) respectively then
356515
Energy levels \(A,B\) and \(C\) of a certain atom correspond to increasing values of energy, i.e.,\({E_A} < {E_B} < {E_C}.\) If \({\lambda _1},{\lambda _2}\) and \({\lambda _3}\) are wavelength corresponding to transitions \(C\) to \(B,B\) to \(A\) and \(C\) to \(A\) respectively then
356515
Energy levels \(A,B\) and \(C\) of a certain atom correspond to increasing values of energy, i.e.,\({E_A} < {E_B} < {E_C}.\) If \({\lambda _1},{\lambda _2}\) and \({\lambda _3}\) are wavelength corresponding to transitions \(C\) to \(B,B\) to \(A\) and \(C\) to \(A\) respectively then
