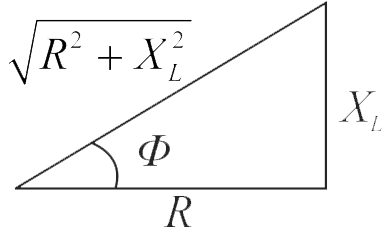
356146 A series LCR circuit with a resistance of \(100 \sqrt{5} \Omega\) is connected to an ac source of \(200\;\,V\). When the capacitor is removed from the circuit, current lags behind emf by \(45^{\circ}\). When the inductor is removed from the circuit keeping the capacitor and resistor in the circuit, current leads by an angle of \(\tan ^{-1}\left(\dfrac{1}{2}\right)\). Calculate the power dissipated in LCR circuit.
356147 A series \(LCR\) circuit is connected to a voltage source. When \(L\) is removed from the circuit, the phase difference between current and voltage is \(\frac{\pi }{3}\). If instead \(C\) is removed from the circuit, the phase difference is again \(\frac{\pi }{3}\) between current and voltage. The power factor of the circuit is:
356146 A series LCR circuit with a resistance of \(100 \sqrt{5} \Omega\) is connected to an ac source of \(200\;\,V\). When the capacitor is removed from the circuit, current lags behind emf by \(45^{\circ}\). When the inductor is removed from the circuit keeping the capacitor and resistor in the circuit, current leads by an angle of \(\tan ^{-1}\left(\dfrac{1}{2}\right)\). Calculate the power dissipated in LCR circuit.
356147 A series \(LCR\) circuit is connected to a voltage source. When \(L\) is removed from the circuit, the phase difference between current and voltage is \(\frac{\pi }{3}\). If instead \(C\) is removed from the circuit, the phase difference is again \(\frac{\pi }{3}\) between current and voltage. The power factor of the circuit is:
356146 A series LCR circuit with a resistance of \(100 \sqrt{5} \Omega\) is connected to an ac source of \(200\;\,V\). When the capacitor is removed from the circuit, current lags behind emf by \(45^{\circ}\). When the inductor is removed from the circuit keeping the capacitor and resistor in the circuit, current leads by an angle of \(\tan ^{-1}\left(\dfrac{1}{2}\right)\). Calculate the power dissipated in LCR circuit.
356147 A series \(LCR\) circuit is connected to a voltage source. When \(L\) is removed from the circuit, the phase difference between current and voltage is \(\frac{\pi }{3}\). If instead \(C\) is removed from the circuit, the phase difference is again \(\frac{\pi }{3}\) between current and voltage. The power factor of the circuit is:
356146 A series LCR circuit with a resistance of \(100 \sqrt{5} \Omega\) is connected to an ac source of \(200\;\,V\). When the capacitor is removed from the circuit, current lags behind emf by \(45^{\circ}\). When the inductor is removed from the circuit keeping the capacitor and resistor in the circuit, current leads by an angle of \(\tan ^{-1}\left(\dfrac{1}{2}\right)\). Calculate the power dissipated in LCR circuit.
356147 A series \(LCR\) circuit is connected to a voltage source. When \(L\) is removed from the circuit, the phase difference between current and voltage is \(\frac{\pi }{3}\). If instead \(C\) is removed from the circuit, the phase difference is again \(\frac{\pi }{3}\) between current and voltage. The power factor of the circuit is: