356129
Assertion :
An electric heater is heated first by direct and then by alternating currents. For both the currents, the potential difference across the ends of the heater is the same. The rate of production of heat will be different in two cases.
Reason :
The resistance of a coil in alternating curent will be more than the resistance of a coil in direct current.
356132
The graph given here represents an idealized sinusoidal current flow between a cloud at a height of 1 \(km\) and the earth, during a lightning discharge. Value of \({I_{0}}\) is 157 \(kA\) and \({T=0.2 {~ms}}\). Assume that discharge happens when the electric field in the air between the cloud and the earth becomes equal to the breakdown field of air i.e., \({E_{0}=3 \times 10^{6} {~V} / {m}}\). Assume that the entire charge on the cloud is released during the lightning and estimate the capacitance of the cloud-Earth system (in \(nF\) ).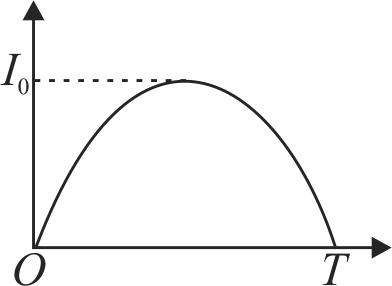
356129
Assertion :
An electric heater is heated first by direct and then by alternating currents. For both the currents, the potential difference across the ends of the heater is the same. The rate of production of heat will be different in two cases.
Reason :
The resistance of a coil in alternating curent will be more than the resistance of a coil in direct current.
356132
The graph given here represents an idealized sinusoidal current flow between a cloud at a height of 1 \(km\) and the earth, during a lightning discharge. Value of \({I_{0}}\) is 157 \(kA\) and \({T=0.2 {~ms}}\). Assume that discharge happens when the electric field in the air between the cloud and the earth becomes equal to the breakdown field of air i.e., \({E_{0}=3 \times 10^{6} {~V} / {m}}\). Assume that the entire charge on the cloud is released during the lightning and estimate the capacitance of the cloud-Earth system (in \(nF\) ).
356129
Assertion :
An electric heater is heated first by direct and then by alternating currents. For both the currents, the potential difference across the ends of the heater is the same. The rate of production of heat will be different in two cases.
Reason :
The resistance of a coil in alternating curent will be more than the resistance of a coil in direct current.
356132
The graph given here represents an idealized sinusoidal current flow between a cloud at a height of 1 \(km\) and the earth, during a lightning discharge. Value of \({I_{0}}\) is 157 \(kA\) and \({T=0.2 {~ms}}\). Assume that discharge happens when the electric field in the air between the cloud and the earth becomes equal to the breakdown field of air i.e., \({E_{0}=3 \times 10^{6} {~V} / {m}}\). Assume that the entire charge on the cloud is released during the lightning and estimate the capacitance of the cloud-Earth system (in \(nF\) ).
356129
Assertion :
An electric heater is heated first by direct and then by alternating currents. For both the currents, the potential difference across the ends of the heater is the same. The rate of production of heat will be different in two cases.
Reason :
The resistance of a coil in alternating curent will be more than the resistance of a coil in direct current.
356132
The graph given here represents an idealized sinusoidal current flow between a cloud at a height of 1 \(km\) and the earth, during a lightning discharge. Value of \({I_{0}}\) is 157 \(kA\) and \({T=0.2 {~ms}}\). Assume that discharge happens when the electric field in the air between the cloud and the earth becomes equal to the breakdown field of air i.e., \({E_{0}=3 \times 10^{6} {~V} / {m}}\). Assume that the entire charge on the cloud is released during the lightning and estimate the capacitance of the cloud-Earth system (in \(nF\) ).
356129
Assertion :
An electric heater is heated first by direct and then by alternating currents. For both the currents, the potential difference across the ends of the heater is the same. The rate of production of heat will be different in two cases.
Reason :
The resistance of a coil in alternating curent will be more than the resistance of a coil in direct current.
356132
The graph given here represents an idealized sinusoidal current flow between a cloud at a height of 1 \(km\) and the earth, during a lightning discharge. Value of \({I_{0}}\) is 157 \(kA\) and \({T=0.2 {~ms}}\). Assume that discharge happens when the electric field in the air between the cloud and the earth becomes equal to the breakdown field of air i.e., \({E_{0}=3 \times 10^{6} {~V} / {m}}\). Assume that the entire charge on the cloud is released during the lightning and estimate the capacitance of the cloud-Earth system (in \(nF\) ).
