282421 Two lenses \(A\) and \(B\) having focal lengths \(2.0 \mathrm{~cm}\) and \(5.0 \mathrm{~cm}\), respectively are placed \(14 \mathrm{~cm}\) apart. Lens \(A\) is placed to the left of lens \(B\). An object is placed \(3 \mathrm{~cm}\) to the left of lens \(A\). The distance of the image from lens \(A\) will be
282423
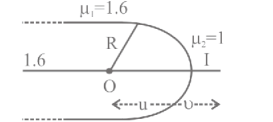
A point object \(O\) is placed on the axis of a cylindrical piece of glass of refractive index 1.6 as shown in the figure. One surface of the glass piece is convex with radius of curvature \(3 \mathrm{~mm}\). The point appeared to be at \(5 \mathrm{~mm}\) on the axis when viewed along the axis and from right side of convex surface. The distance of the point object from the convex surface is :
282421 Two lenses \(A\) and \(B\) having focal lengths \(2.0 \mathrm{~cm}\) and \(5.0 \mathrm{~cm}\), respectively are placed \(14 \mathrm{~cm}\) apart. Lens \(A\) is placed to the left of lens \(B\). An object is placed \(3 \mathrm{~cm}\) to the left of lens \(A\). The distance of the image from lens \(A\) will be
282423
A point object \(O\) is placed on the axis of a cylindrical piece of glass of refractive index 1.6 as shown in the figure. One surface of the glass piece is convex with radius of curvature \(3 \mathrm{~mm}\). The point appeared to be at \(5 \mathrm{~mm}\) on the axis when viewed along the axis and from right side of convex surface. The distance of the point object from the convex surface is :

282421 Two lenses \(A\) and \(B\) having focal lengths \(2.0 \mathrm{~cm}\) and \(5.0 \mathrm{~cm}\), respectively are placed \(14 \mathrm{~cm}\) apart. Lens \(A\) is placed to the left of lens \(B\). An object is placed \(3 \mathrm{~cm}\) to the left of lens \(A\). The distance of the image from lens \(A\) will be
282423
A point object \(O\) is placed on the axis of a cylindrical piece of glass of refractive index 1.6 as shown in the figure. One surface of the glass piece is convex with radius of curvature \(3 \mathrm{~mm}\). The point appeared to be at \(5 \mathrm{~mm}\) on the axis when viewed along the axis and from right side of convex surface. The distance of the point object from the convex surface is :

282421 Two lenses \(A\) and \(B\) having focal lengths \(2.0 \mathrm{~cm}\) and \(5.0 \mathrm{~cm}\), respectively are placed \(14 \mathrm{~cm}\) apart. Lens \(A\) is placed to the left of lens \(B\). An object is placed \(3 \mathrm{~cm}\) to the left of lens \(A\). The distance of the image from lens \(A\) will be
282423
A point object \(O\) is placed on the axis of a cylindrical piece of glass of refractive index 1.6 as shown in the figure. One surface of the glass piece is convex with radius of curvature \(3 \mathrm{~mm}\). The point appeared to be at \(5 \mathrm{~mm}\) on the axis when viewed along the axis and from right side of convex surface. The distance of the point object from the convex surface is :

282421 Two lenses \(A\) and \(B\) having focal lengths \(2.0 \mathrm{~cm}\) and \(5.0 \mathrm{~cm}\), respectively are placed \(14 \mathrm{~cm}\) apart. Lens \(A\) is placed to the left of lens \(B\). An object is placed \(3 \mathrm{~cm}\) to the left of lens \(A\). The distance of the image from lens \(A\) will be
282423
A point object \(O\) is placed on the axis of a cylindrical piece of glass of refractive index 1.6 as shown in the figure. One surface of the glass piece is convex with radius of curvature \(3 \mathrm{~mm}\). The point appeared to be at \(5 \mathrm{~mm}\) on the axis when viewed along the axis and from right side of convex surface. The distance of the point object from the convex surface is :



