281995
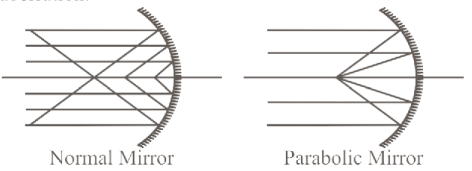
In a reflecting astronomical telescope, parabolic mirrors are used because they are free from
1 spherical aberration
2 chromatic aberration
3 both spherical and chromatic aberration
4 no aberration
Explanation:
C: Parabolic mirror are used in a reflection astronomical telescope, because
1. This mirror is designed to be free of spherical aberration.
AMU-2002
Ray Optics
281996
Ray optics is valid, when characteristic dimensions are
1 of the same order as the wavelength of light
2 much smaller than the wavelength of light
3 of the order of one millimetre
4 much larger than the wavelength of light
Explanation:
D: In ray optics, characteristic dimensions should be much larger than the wavelength of light because if size of object is comparable to wavelength of light, then diffraction could happen. But for that it will require wave theory of light.
UP CPMT-2009
Ray Optics
281997
A ray of light strikes a material's slab at an angle of incidence $60^{\circ}$. If the reflected and refracted rays are perpendicular to each other, the refractive index of the material is
1 $\frac{1}{\sqrt{3}}$
2 $\frac{1}{\sqrt{2}}$
3 $\sqrt{2}$
4 $\sqrt{3}$
Explanation:
D:
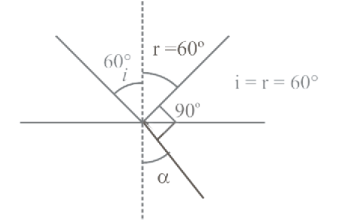
Let refracted ray is $\alpha$ and refractive index of the material be $\mu_2$
According to question,
$\begin{aligned}
r+90^{\circ}+\alpha=180^{\circ} \\
60^{\circ}+90^{\circ}+\alpha=180^{\circ} \\
\alpha=30^{\circ}
\end{aligned}$
From snell's law
$\begin{aligned}
\mu_1 \sin i=\mu_2 \sin \alpha \\
\mu_2=\frac{\sin i}{\sin \alpha} \\
\mu_2=\frac{\sin 60^{\circ}}{\sin 30^{\circ}} \\
\mu_2=\sqrt{3}
\end{aligned} \quad\left(\because \mu_1=1 \text { for air }\right)$
DCE-2009
Ray Optics
281998
The difference in the number of wavelengths. When yellow light propagates through air and vacuum columns of the same thickness, is one The thickness of the air column is
Refractive index of air $\mu=1.0003$, wavelength of yellow light in vacuum $=6000 \AA$
1 $1.8 \mathrm{~mm}$
2 $2 \mathrm{~mm}$
3 $2 \mathrm{~cm}$
4 $2.2 \mathrm{~cm}$
Explanation:
B: Let the thickness of the air column $=\mathrm{L}$
Wavelength of yellow light in vacuum $\left(\lambda_{\mathrm{v}}\right)=6000 \AA$ $6000 \times 10^{-10} \mathrm{~m}$
Refractive index of air $(\mu)=1.0003$.
Difference in number of wavelengths $=1$
$\begin{aligned}
\mathrm{n}_{\mathrm{a}}-\mathrm{n}_{\mathrm{v}}=1 \\
\frac{\mathrm{L}}{\lambda_{\mathrm{a}}}-\frac{\mathrm{L}}{\lambda_{\mathrm{v}}}=1 \\
\mathrm{~L}\left(\frac{1}{\lambda_{\mathrm{a}}}-\frac{1}{\lambda_{\mathrm{v}}}\right)=1
\end{aligned} \quad\left(\because \mathrm{n}=\frac{1}{\lambda}\right)$
We know, Refractive index
$\begin{aligned}
\mu=\frac{\mathrm{c}}{\mathrm{V}}=\frac{\lambda_{\mathrm{v}}}{\lambda_{\mathrm{a}}} \\
\lambda_{\mathrm{a}}=\frac{\lambda_{\mathrm{v}}}{\mu}
\end{aligned}$
From equation (i)
$\begin{array}{l}
\mathrm{L}\left(\frac{1}{\frac{\lambda_{\mathrm{v}}}{\mu}}-\frac{1}{\lambda_{\mathrm{v}}}\right)=1 \\
\frac{\mathrm{L}}{\lambda_{\mathrm{v}}}(\mu-1)=1 \\
\mathrm{~L}=\frac{1}{(\mu-1)} \times \lambda_{\mathrm{v}} \\
\mathrm{L}=\frac{6000 \times 10^{-10}}{(1.0003-1)} \\
\mathrm{L}=\frac{6000 \times 10^{-10}}{3 \times 10^{-4}} \\
\mathrm{~L}=2000 \times 10^{-6}=2 \times 10^{-3} \mathrm{~m} \\
\mathrm{~L}=2 \mathrm{~mm}
\end{array}$
281995
In a reflecting astronomical telescope, parabolic mirrors are used because they are free from
1 spherical aberration
2 chromatic aberration
3 both spherical and chromatic aberration
4 no aberration
Explanation:
C: Parabolic mirror are used in a reflection astronomical telescope, because
1. This mirror is designed to be free of spherical aberration.
AMU-2002
Ray Optics
281996
Ray optics is valid, when characteristic dimensions are

1 of the same order as the wavelength of light
2 much smaller than the wavelength of light
3 of the order of one millimetre
4 much larger than the wavelength of light
Explanation:
D: In ray optics, characteristic dimensions should be much larger than the wavelength of light because if size of object is comparable to wavelength of light, then diffraction could happen. But for that it will require wave theory of light.
UP CPMT-2009
Ray Optics
281997
A ray of light strikes a material's slab at an angle of incidence $60^{\circ}$. If the reflected and refracted rays are perpendicular to each other, the refractive index of the material is
1 $\frac{1}{\sqrt{3}}$
2 $\frac{1}{\sqrt{2}}$
3 $\sqrt{2}$
4 $\sqrt{3}$
Explanation:
D:

Let refracted ray is $\alpha$ and refractive index of the material be $\mu_2$
According to question,
$\begin{aligned}
r+90^{\circ}+\alpha=180^{\circ} \\
60^{\circ}+90^{\circ}+\alpha=180^{\circ} \\
\alpha=30^{\circ}
\end{aligned}$
From snell's law
$\begin{aligned}
\mu_1 \sin i=\mu_2 \sin \alpha \\
\mu_2=\frac{\sin i}{\sin \alpha} \\
\mu_2=\frac{\sin 60^{\circ}}{\sin 30^{\circ}} \\
\mu_2=\sqrt{3}
\end{aligned} \quad\left(\because \mu_1=1 \text { for air }\right)$
DCE-2009
Ray Optics
281998
The difference in the number of wavelengths. When yellow light propagates through air and vacuum columns of the same thickness, is one The thickness of the air column is
Refractive index of air $\mu=1.0003$, wavelength of yellow light in vacuum $=6000 \AA$
1 $1.8 \mathrm{~mm}$
2 $2 \mathrm{~mm}$
3 $2 \mathrm{~cm}$
4 $2.2 \mathrm{~cm}$
Explanation:
B: Let the thickness of the air column $=\mathrm{L}$
Wavelength of yellow light in vacuum $\left(\lambda_{\mathrm{v}}\right)=6000 \AA$ $6000 \times 10^{-10} \mathrm{~m}$
Refractive index of air $(\mu)=1.0003$.
Difference in number of wavelengths $=1$
$\begin{aligned}
\mathrm{n}_{\mathrm{a}}-\mathrm{n}_{\mathrm{v}}=1 \\
\frac{\mathrm{L}}{\lambda_{\mathrm{a}}}-\frac{\mathrm{L}}{\lambda_{\mathrm{v}}}=1 \\
\mathrm{~L}\left(\frac{1}{\lambda_{\mathrm{a}}}-\frac{1}{\lambda_{\mathrm{v}}}\right)=1
\end{aligned} \quad\left(\because \mathrm{n}=\frac{1}{\lambda}\right)$
We know, Refractive index
$\begin{aligned}
\mu=\frac{\mathrm{c}}{\mathrm{V}}=\frac{\lambda_{\mathrm{v}}}{\lambda_{\mathrm{a}}} \\
\lambda_{\mathrm{a}}=\frac{\lambda_{\mathrm{v}}}{\mu}
\end{aligned}$
From equation (i)
$\begin{array}{l}
\mathrm{L}\left(\frac{1}{\frac{\lambda_{\mathrm{v}}}{\mu}}-\frac{1}{\lambda_{\mathrm{v}}}\right)=1 \\
\frac{\mathrm{L}}{\lambda_{\mathrm{v}}}(\mu-1)=1 \\
\mathrm{~L}=\frac{1}{(\mu-1)} \times \lambda_{\mathrm{v}} \\
\mathrm{L}=\frac{6000 \times 10^{-10}}{(1.0003-1)} \\
\mathrm{L}=\frac{6000 \times 10^{-10}}{3 \times 10^{-4}} \\
\mathrm{~L}=2000 \times 10^{-6}=2 \times 10^{-3} \mathrm{~m} \\
\mathrm{~L}=2 \mathrm{~mm}
\end{array}$
281995
In a reflecting astronomical telescope, parabolic mirrors are used because they are free from
1 spherical aberration
2 chromatic aberration
3 both spherical and chromatic aberration
4 no aberration
Explanation:
C: Parabolic mirror are used in a reflection astronomical telescope, because
1. This mirror is designed to be free of spherical aberration.
AMU-2002
Ray Optics
281996
Ray optics is valid, when characteristic dimensions are

1 of the same order as the wavelength of light
2 much smaller than the wavelength of light
3 of the order of one millimetre
4 much larger than the wavelength of light
Explanation:
D: In ray optics, characteristic dimensions should be much larger than the wavelength of light because if size of object is comparable to wavelength of light, then diffraction could happen. But for that it will require wave theory of light.
UP CPMT-2009
Ray Optics
281997
A ray of light strikes a material's slab at an angle of incidence $60^{\circ}$. If the reflected and refracted rays are perpendicular to each other, the refractive index of the material is
1 $\frac{1}{\sqrt{3}}$
2 $\frac{1}{\sqrt{2}}$
3 $\sqrt{2}$
4 $\sqrt{3}$
Explanation:
D:

Let refracted ray is $\alpha$ and refractive index of the material be $\mu_2$
According to question,
$\begin{aligned}
r+90^{\circ}+\alpha=180^{\circ} \\
60^{\circ}+90^{\circ}+\alpha=180^{\circ} \\
\alpha=30^{\circ}
\end{aligned}$
From snell's law
$\begin{aligned}
\mu_1 \sin i=\mu_2 \sin \alpha \\
\mu_2=\frac{\sin i}{\sin \alpha} \\
\mu_2=\frac{\sin 60^{\circ}}{\sin 30^{\circ}} \\
\mu_2=\sqrt{3}
\end{aligned} \quad\left(\because \mu_1=1 \text { for air }\right)$
DCE-2009
Ray Optics
281998
The difference in the number of wavelengths. When yellow light propagates through air and vacuum columns of the same thickness, is one The thickness of the air column is
Refractive index of air $\mu=1.0003$, wavelength of yellow light in vacuum $=6000 \AA$
1 $1.8 \mathrm{~mm}$
2 $2 \mathrm{~mm}$
3 $2 \mathrm{~cm}$
4 $2.2 \mathrm{~cm}$
Explanation:
B: Let the thickness of the air column $=\mathrm{L}$
Wavelength of yellow light in vacuum $\left(\lambda_{\mathrm{v}}\right)=6000 \AA$ $6000 \times 10^{-10} \mathrm{~m}$
Refractive index of air $(\mu)=1.0003$.
Difference in number of wavelengths $=1$
$\begin{aligned}
\mathrm{n}_{\mathrm{a}}-\mathrm{n}_{\mathrm{v}}=1 \\
\frac{\mathrm{L}}{\lambda_{\mathrm{a}}}-\frac{\mathrm{L}}{\lambda_{\mathrm{v}}}=1 \\
\mathrm{~L}\left(\frac{1}{\lambda_{\mathrm{a}}}-\frac{1}{\lambda_{\mathrm{v}}}\right)=1
\end{aligned} \quad\left(\because \mathrm{n}=\frac{1}{\lambda}\right)$
We know, Refractive index
$\begin{aligned}
\mu=\frac{\mathrm{c}}{\mathrm{V}}=\frac{\lambda_{\mathrm{v}}}{\lambda_{\mathrm{a}}} \\
\lambda_{\mathrm{a}}=\frac{\lambda_{\mathrm{v}}}{\mu}
\end{aligned}$
From equation (i)
$\begin{array}{l}
\mathrm{L}\left(\frac{1}{\frac{\lambda_{\mathrm{v}}}{\mu}}-\frac{1}{\lambda_{\mathrm{v}}}\right)=1 \\
\frac{\mathrm{L}}{\lambda_{\mathrm{v}}}(\mu-1)=1 \\
\mathrm{~L}=\frac{1}{(\mu-1)} \times \lambda_{\mathrm{v}} \\
\mathrm{L}=\frac{6000 \times 10^{-10}}{(1.0003-1)} \\
\mathrm{L}=\frac{6000 \times 10^{-10}}{3 \times 10^{-4}} \\
\mathrm{~L}=2000 \times 10^{-6}=2 \times 10^{-3} \mathrm{~m} \\
\mathrm{~L}=2 \mathrm{~mm}
\end{array}$
NEET Test Series from KOTA - 10 Papers In MS WORD
WhatsApp Here
Ray Optics
281995
In a reflecting astronomical telescope, parabolic mirrors are used because they are free from
1 spherical aberration
2 chromatic aberration
3 both spherical and chromatic aberration
4 no aberration
Explanation:
C: Parabolic mirror are used in a reflection astronomical telescope, because
1. This mirror is designed to be free of spherical aberration.
AMU-2002
Ray Optics
281996
Ray optics is valid, when characteristic dimensions are

1 of the same order as the wavelength of light
2 much smaller than the wavelength of light
3 of the order of one millimetre
4 much larger than the wavelength of light
Explanation:
D: In ray optics, characteristic dimensions should be much larger than the wavelength of light because if size of object is comparable to wavelength of light, then diffraction could happen. But for that it will require wave theory of light.
UP CPMT-2009
Ray Optics
281997
A ray of light strikes a material's slab at an angle of incidence $60^{\circ}$. If the reflected and refracted rays are perpendicular to each other, the refractive index of the material is
1 $\frac{1}{\sqrt{3}}$
2 $\frac{1}{\sqrt{2}}$
3 $\sqrt{2}$
4 $\sqrt{3}$
Explanation:
D:

Let refracted ray is $\alpha$ and refractive index of the material be $\mu_2$
According to question,
$\begin{aligned}
r+90^{\circ}+\alpha=180^{\circ} \\
60^{\circ}+90^{\circ}+\alpha=180^{\circ} \\
\alpha=30^{\circ}
\end{aligned}$
From snell's law
$\begin{aligned}
\mu_1 \sin i=\mu_2 \sin \alpha \\
\mu_2=\frac{\sin i}{\sin \alpha} \\
\mu_2=\frac{\sin 60^{\circ}}{\sin 30^{\circ}} \\
\mu_2=\sqrt{3}
\end{aligned} \quad\left(\because \mu_1=1 \text { for air }\right)$
DCE-2009
Ray Optics
281998
The difference in the number of wavelengths. When yellow light propagates through air and vacuum columns of the same thickness, is one The thickness of the air column is
Refractive index of air $\mu=1.0003$, wavelength of yellow light in vacuum $=6000 \AA$
1 $1.8 \mathrm{~mm}$
2 $2 \mathrm{~mm}$
3 $2 \mathrm{~cm}$
4 $2.2 \mathrm{~cm}$
Explanation:
B: Let the thickness of the air column $=\mathrm{L}$
Wavelength of yellow light in vacuum $\left(\lambda_{\mathrm{v}}\right)=6000 \AA$ $6000 \times 10^{-10} \mathrm{~m}$
Refractive index of air $(\mu)=1.0003$.
Difference in number of wavelengths $=1$
$\begin{aligned}
\mathrm{n}_{\mathrm{a}}-\mathrm{n}_{\mathrm{v}}=1 \\
\frac{\mathrm{L}}{\lambda_{\mathrm{a}}}-\frac{\mathrm{L}}{\lambda_{\mathrm{v}}}=1 \\
\mathrm{~L}\left(\frac{1}{\lambda_{\mathrm{a}}}-\frac{1}{\lambda_{\mathrm{v}}}\right)=1
\end{aligned} \quad\left(\because \mathrm{n}=\frac{1}{\lambda}\right)$
We know, Refractive index
$\begin{aligned}
\mu=\frac{\mathrm{c}}{\mathrm{V}}=\frac{\lambda_{\mathrm{v}}}{\lambda_{\mathrm{a}}} \\
\lambda_{\mathrm{a}}=\frac{\lambda_{\mathrm{v}}}{\mu}
\end{aligned}$
From equation (i)
$\begin{array}{l}
\mathrm{L}\left(\frac{1}{\frac{\lambda_{\mathrm{v}}}{\mu}}-\frac{1}{\lambda_{\mathrm{v}}}\right)=1 \\
\frac{\mathrm{L}}{\lambda_{\mathrm{v}}}(\mu-1)=1 \\
\mathrm{~L}=\frac{1}{(\mu-1)} \times \lambda_{\mathrm{v}} \\
\mathrm{L}=\frac{6000 \times 10^{-10}}{(1.0003-1)} \\
\mathrm{L}=\frac{6000 \times 10^{-10}}{3 \times 10^{-4}} \\
\mathrm{~L}=2000 \times 10^{-6}=2 \times 10^{-3} \mathrm{~m} \\
\mathrm{~L}=2 \mathrm{~mm}
\end{array}$