281929
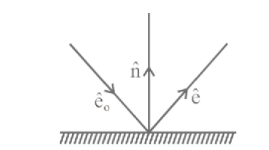
A ray of light is reflected by a plane mirror. $\hat{\mathbf{e}}_0, \hat{\mathrm{e}}$ and $\hat{\mathbf{n}}$ be the unit vectors along the incident ray, reflected ray and the normal to the reflecting surface respectively.
Which of the following gives an expression for $\hat{\mathrm{e}}$ ?
281930 A girl of height $150 \mathrm{~cm}$ with her eye level at 140 $\mathrm{cm}$ stands in front of plane mirror of height $\mathbf{7 5}$ $\mathrm{cm}$ fixed to a wall. The lower edge of the mirror is at a height of $85 \mathrm{~cm}$ above her feet level. The height of her image the girl can see in the mirror is
281929
A ray of light is reflected by a plane mirror. $\hat{\mathbf{e}}_0, \hat{\mathrm{e}}$ and $\hat{\mathbf{n}}$ be the unit vectors along the incident ray, reflected ray and the normal to the reflecting surface respectively.
Which of the following gives an expression for $\hat{\mathrm{e}}$ ?

281930 A girl of height $150 \mathrm{~cm}$ with her eye level at 140 $\mathrm{cm}$ stands in front of plane mirror of height $\mathbf{7 5}$ $\mathrm{cm}$ fixed to a wall. The lower edge of the mirror is at a height of $85 \mathrm{~cm}$ above her feet level. The height of her image the girl can see in the mirror is
281929
A ray of light is reflected by a plane mirror. $\hat{\mathbf{e}}_0, \hat{\mathrm{e}}$ and $\hat{\mathbf{n}}$ be the unit vectors along the incident ray, reflected ray and the normal to the reflecting surface respectively.
Which of the following gives an expression for $\hat{\mathrm{e}}$ ?

281930 A girl of height $150 \mathrm{~cm}$ with her eye level at 140 $\mathrm{cm}$ stands in front of plane mirror of height $\mathbf{7 5}$ $\mathrm{cm}$ fixed to a wall. The lower edge of the mirror is at a height of $85 \mathrm{~cm}$ above her feet level. The height of her image the girl can see in the mirror is
281929
A ray of light is reflected by a plane mirror. $\hat{\mathbf{e}}_0, \hat{\mathrm{e}}$ and $\hat{\mathbf{n}}$ be the unit vectors along the incident ray, reflected ray and the normal to the reflecting surface respectively.
Which of the following gives an expression for $\hat{\mathrm{e}}$ ?

281930 A girl of height $150 \mathrm{~cm}$ with her eye level at 140 $\mathrm{cm}$ stands in front of plane mirror of height $\mathbf{7 5}$ $\mathrm{cm}$ fixed to a wall. The lower edge of the mirror is at a height of $85 \mathrm{~cm}$ above her feet level. The height of her image the girl can see in the mirror is