270389
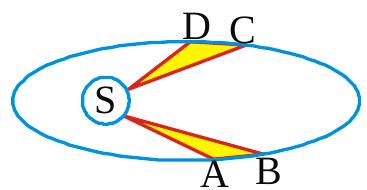
The motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time ' \(t_{1}\) ' and ' \(t_{2}\) ' in moving from \(\mathbf{A}\) to \(\mathrm{B}\) and from \(\mathbf{C}\) to \(\mathbf{D}\) respectively, then
270389
The motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time ' \(t_{1}\) ' and ' \(t_{2}\) ' in moving from \(\mathbf{A}\) to \(\mathrm{B}\) and from \(\mathbf{C}\) to \(\mathbf{D}\) respectively, then

270389
The motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time ' \(t_{1}\) ' and ' \(t_{2}\) ' in moving from \(\mathbf{A}\) to \(\mathrm{B}\) and from \(\mathbf{C}\) to \(\mathbf{D}\) respectively, then

270389
The motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time ' \(t_{1}\) ' and ' \(t_{2}\) ' in moving from \(\mathbf{A}\) to \(\mathrm{B}\) and from \(\mathbf{C}\) to \(\mathbf{D}\) respectively, then
