270378
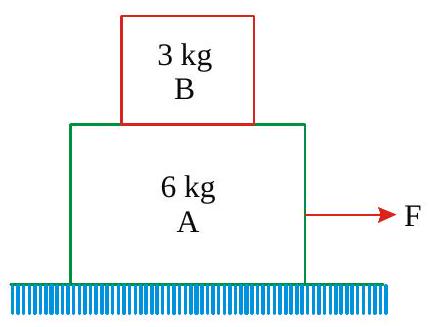
Find the least horizontal force \(P\) to start motion of any part of the system of the three blocks resting upon one another as shown in fig. The weights of blocks are\(A=300 \mathrm{~N}, B=100 \mathrm{~N}\) and \(C=200 \mathrm{~N}\). Between \(A\) and \(B\), coefficient of friction is 0.3 , between \(B\) and \(C\) is 0.2 and between \(C\) and the ground is 0.1 .
270378
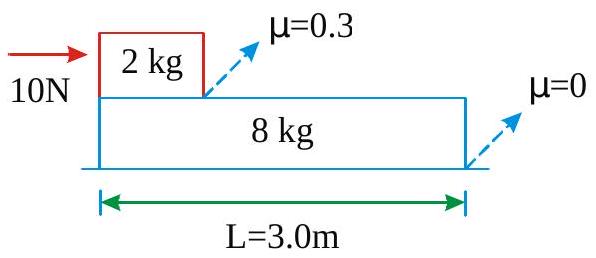
Find the least horizontal force \(P\) to start motion of any part of the system of the three blocks resting upon one another as shown in fig. The weights of blocks are\(A=300 \mathrm{~N}, B=100 \mathrm{~N}\) and \(C=200 \mathrm{~N}\). Between \(A\) and \(B\), coefficient of friction is 0.3 , between \(B\) and \(C\) is 0.2 and between \(C\) and the ground is 0.1 .

270378
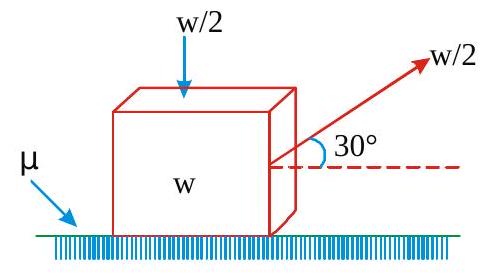
Find the least horizontal force \(P\) to start motion of any part of the system of the three blocks resting upon one another as shown in fig. The weights of blocks are\(A=300 \mathrm{~N}, B=100 \mathrm{~N}\) and \(C=200 \mathrm{~N}\). Between \(A\) and \(B\), coefficient of friction is 0.3 , between \(B\) and \(C\) is 0.2 and between \(C\) and the ground is 0.1 .

270378
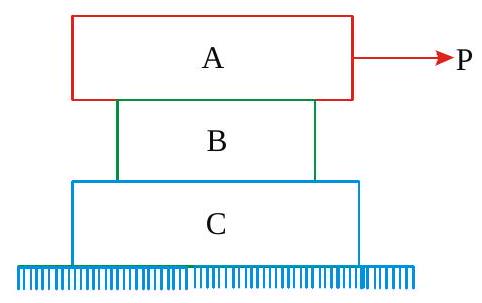
Find the least horizontal force \(P\) to start motion of any part of the system of the three blocks resting upon one another as shown in fig. The weights of blocks are\(A=300 \mathrm{~N}, B=100 \mathrm{~N}\) and \(C=200 \mathrm{~N}\). Between \(A\) and \(B\), coefficient of friction is 0.3 , between \(B\) and \(C\) is 0.2 and between \(C\) and the ground is 0.1 .