270369
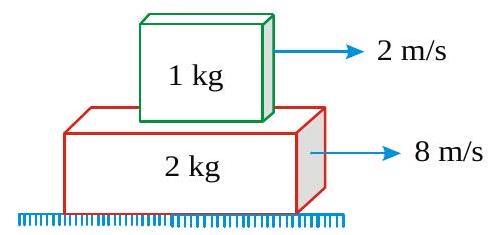
Coefficient of friction between two blocks shown in figure is \(\mu=0.4\). the blocks are given velocities of \(2 \mathrm{~m} / \mathrm{s}\) and \(8 \mathrm{~m} / \mathrm{s}\) in the directions shown in figure. Find.
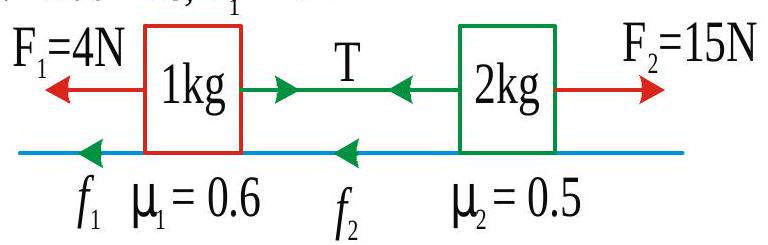
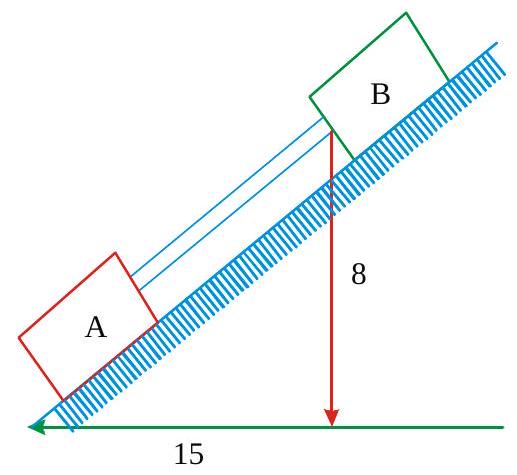
Two blocks\(A\) and \(B\) are separated by some distance and tied by a string as shown in the figure. The force of friction in both the blocks at \(\mathrm{t}=2 \mathrm{~s}\) is.
270375 A suitcase is gently dropped on a conveyor belt moving at a velocity of\(3 \mathrm{~m} / \mathrm{s}\). If the coefficient of friction between the belt and the suitcase is 0.5 , find the displacement of the suitcase relative to conveyor belt before the slipping between the two is stopped \(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)
270376
Blocks\(A\) and \(B\) in the fig, are connected by a bar of negligible weight. Mass of each block is \(170 \mathrm{~kg}\) and \(\mu_{A}=0.2\) and \(\mu_{B}=0.4\), where \(\mu_{A}\) and \(\mu_{B}\) are the coefficients of limiting friction between blocks and plane. Calculate the force developed in the bar \(\left(g=10 \mathrm{~m} / \mathrm{sec}^{2}\right)\).
270369
Coefficient of friction between two blocks shown in figure is \(\mu=0.4\). the blocks are given velocities of \(2 \mathrm{~m} / \mathrm{s}\) and \(8 \mathrm{~m} / \mathrm{s}\) in the directions shown in figure. Find.

Two blocks\(A\) and \(B\) are separated by some distance and tied by a string as shown in the figure. The force of friction in both the blocks at \(\mathrm{t}=2 \mathrm{~s}\) is.

270375 A suitcase is gently dropped on a conveyor belt moving at a velocity of\(3 \mathrm{~m} / \mathrm{s}\). If the coefficient of friction between the belt and the suitcase is 0.5 , find the displacement of the suitcase relative to conveyor belt before the slipping between the two is stopped \(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)
270376
Blocks\(A\) and \(B\) in the fig, are connected by a bar of negligible weight. Mass of each block is \(170 \mathrm{~kg}\) and \(\mu_{A}=0.2\) and \(\mu_{B}=0.4\), where \(\mu_{A}\) and \(\mu_{B}\) are the coefficients of limiting friction between blocks and plane. Calculate the force developed in the bar \(\left(g=10 \mathrm{~m} / \mathrm{sec}^{2}\right)\).

270369
Coefficient of friction between two blocks shown in figure is \(\mu=0.4\). the blocks are given velocities of \(2 \mathrm{~m} / \mathrm{s}\) and \(8 \mathrm{~m} / \mathrm{s}\) in the directions shown in figure. Find.

Two blocks\(A\) and \(B\) are separated by some distance and tied by a string as shown in the figure. The force of friction in both the blocks at \(\mathrm{t}=2 \mathrm{~s}\) is.

270375 A suitcase is gently dropped on a conveyor belt moving at a velocity of\(3 \mathrm{~m} / \mathrm{s}\). If the coefficient of friction between the belt and the suitcase is 0.5 , find the displacement of the suitcase relative to conveyor belt before the slipping between the two is stopped \(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)
270376
Blocks\(A\) and \(B\) in the fig, are connected by a bar of negligible weight. Mass of each block is \(170 \mathrm{~kg}\) and \(\mu_{A}=0.2\) and \(\mu_{B}=0.4\), where \(\mu_{A}\) and \(\mu_{B}\) are the coefficients of limiting friction between blocks and plane. Calculate the force developed in the bar \(\left(g=10 \mathrm{~m} / \mathrm{sec}^{2}\right)\).

270369
Coefficient of friction between two blocks shown in figure is \(\mu=0.4\). the blocks are given velocities of \(2 \mathrm{~m} / \mathrm{s}\) and \(8 \mathrm{~m} / \mathrm{s}\) in the directions shown in figure. Find.

Two blocks\(A\) and \(B\) are separated by some distance and tied by a string as shown in the figure. The force of friction in both the blocks at \(\mathrm{t}=2 \mathrm{~s}\) is.

270375 A suitcase is gently dropped on a conveyor belt moving at a velocity of\(3 \mathrm{~m} / \mathrm{s}\). If the coefficient of friction between the belt and the suitcase is 0.5 , find the displacement of the suitcase relative to conveyor belt before the slipping between the two is stopped \(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)
270376
Blocks\(A\) and \(B\) in the fig, are connected by a bar of negligible weight. Mass of each block is \(170 \mathrm{~kg}\) and \(\mu_{A}=0.2\) and \(\mu_{B}=0.4\), where \(\mu_{A}\) and \(\mu_{B}\) are the coefficients of limiting friction between blocks and plane. Calculate the force developed in the bar \(\left(g=10 \mathrm{~m} / \mathrm{sec}^{2}\right)\).

270369
Coefficient of friction between two blocks shown in figure is \(\mu=0.4\). the blocks are given velocities of \(2 \mathrm{~m} / \mathrm{s}\) and \(8 \mathrm{~m} / \mathrm{s}\) in the directions shown in figure. Find.

Two blocks\(A\) and \(B\) are separated by some distance and tied by a string as shown in the figure. The force of friction in both the blocks at \(\mathrm{t}=2 \mathrm{~s}\) is.

270375 A suitcase is gently dropped on a conveyor belt moving at a velocity of\(3 \mathrm{~m} / \mathrm{s}\). If the coefficient of friction between the belt and the suitcase is 0.5 , find the displacement of the suitcase relative to conveyor belt before the slipping between the two is stopped \(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)
270376
Blocks\(A\) and \(B\) in the fig, are connected by a bar of negligible weight. Mass of each block is \(170 \mathrm{~kg}\) and \(\mu_{A}=0.2\) and \(\mu_{B}=0.4\), where \(\mu_{A}\) and \(\mu_{B}\) are the coefficients of limiting friction between blocks and plane. Calculate the force developed in the bar \(\left(g=10 \mathrm{~m} / \mathrm{sec}^{2}\right)\).