270207 A pendulum bob is hanging from the roof of an elevator with the help of a light string. When the elevator moves up with uniform acceleration '\(a\) ' the tension in the string is \(T_{1}\). When the elevator moves down with the same acceleration, the tension in the string is \(T_{2}\).If the elevator were stationary, the tension in the string would be
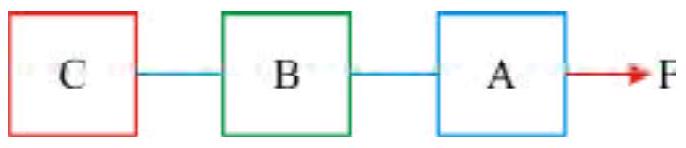
270208 Three bodies are lying on a frictionless horizontal table and theseare connected as shown in the figure. They are pulled towards right with a force \(T_{3}=60 \mathrm{~N}\) If \(m_{1} m_{2}\) and \(m_{3}\) are equal to \(10 \mathrm{~kg}, 20 \mathrm{~kg}\) and \(30 \mathrm{~kg}\) respectively, then the values of \(T_{1}\) and \(T_{2}\) will be
270207 A pendulum bob is hanging from the roof of an elevator with the help of a light string. When the elevator moves up with uniform acceleration '\(a\) ' the tension in the string is \(T_{1}\). When the elevator moves down with the same acceleration, the tension in the string is \(T_{2}\).If the elevator were stationary, the tension in the string would be
270208 Three bodies are lying on a frictionless horizontal table and theseare connected as shown in the figure. They are pulled towards right with a force \(T_{3}=60 \mathrm{~N}\) If \(m_{1} m_{2}\) and \(m_{3}\) are equal to \(10 \mathrm{~kg}, 20 \mathrm{~kg}\) and \(30 \mathrm{~kg}\) respectively, then the values of \(T_{1}\) and \(T_{2}\) will be
270207 A pendulum bob is hanging from the roof of an elevator with the help of a light string. When the elevator moves up with uniform acceleration '\(a\) ' the tension in the string is \(T_{1}\). When the elevator moves down with the same acceleration, the tension in the string is \(T_{2}\).If the elevator were stationary, the tension in the string would be
270208 Three bodies are lying on a frictionless horizontal table and theseare connected as shown in the figure. They are pulled towards right with a force \(T_{3}=60 \mathrm{~N}\) If \(m_{1} m_{2}\) and \(m_{3}\) are equal to \(10 \mathrm{~kg}, 20 \mathrm{~kg}\) and \(30 \mathrm{~kg}\) respectively, then the values of \(T_{1}\) and \(T_{2}\) will be
270207 A pendulum bob is hanging from the roof of an elevator with the help of a light string. When the elevator moves up with uniform acceleration '\(a\) ' the tension in the string is \(T_{1}\). When the elevator moves down with the same acceleration, the tension in the string is \(T_{2}\).If the elevator were stationary, the tension in the string would be
270208 Three bodies are lying on a frictionless horizontal table and theseare connected as shown in the figure. They are pulled towards right with a force \(T_{3}=60 \mathrm{~N}\) If \(m_{1} m_{2}\) and \(m_{3}\) are equal to \(10 \mathrm{~kg}, 20 \mathrm{~kg}\) and \(30 \mathrm{~kg}\) respectively, then the values of \(T_{1}\) and \(T_{2}\) will be
270207 A pendulum bob is hanging from the roof of an elevator with the help of a light string. When the elevator moves up with uniform acceleration '\(a\) ' the tension in the string is \(T_{1}\). When the elevator moves down with the same acceleration, the tension in the string is \(T_{2}\).If the elevator were stationary, the tension in the string would be
270208 Three bodies are lying on a frictionless horizontal table and theseare connected as shown in the figure. They are pulled towards right with a force \(T_{3}=60 \mathrm{~N}\) If \(m_{1} m_{2}\) and \(m_{3}\) are equal to \(10 \mathrm{~kg}, 20 \mathrm{~kg}\) and \(30 \mathrm{~kg}\) respectively, then the values of \(T_{1}\) and \(T_{2}\) will be