270230
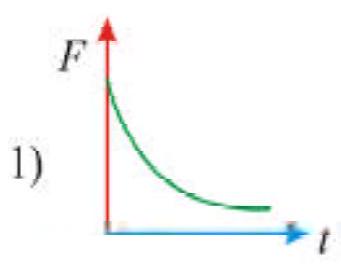
Two blocks of masses\(m\) and \(M\) are placed on a horizontal frictionless table connected by light spring as shown in the figure . Mass \(M\) is pulled to the right with a force \(F\). If the acceleration of mass \(\mathrm{m}\) is \(a\), then the acceleration of mass \(M\) will be (AIEEE-2007)

270230
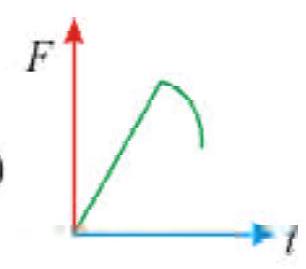
Two blocks of masses\(m\) and \(M\) are placed on a horizontal frictionless table connected by light spring as shown in the figure . Mass \(M\) is pulled to the right with a force \(F\). If the acceleration of mass \(\mathrm{m}\) is \(a\), then the acceleration of mass \(M\) will be (AIEEE-2007)

270230
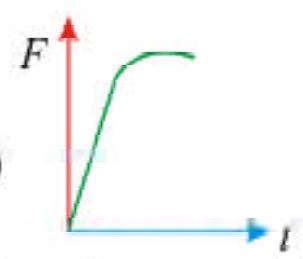
Two blocks of masses\(m\) and \(M\) are placed on a horizontal frictionless table connected by light spring as shown in the figure . Mass \(M\) is pulled to the right with a force \(F\). If the acceleration of mass \(\mathrm{m}\) is \(a\), then the acceleration of mass \(M\) will be (AIEEE-2007)

270230
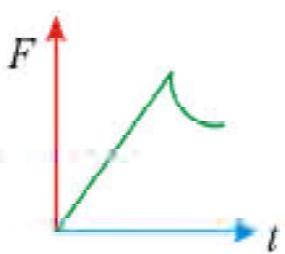
Two blocks of masses\(m\) and \(M\) are placed on a horizontal frictionless table connected by light spring as shown in the figure . Mass \(M\) is pulled to the right with a force \(F\). If the acceleration of mass \(\mathrm{m}\) is \(a\), then the acceleration of mass \(M\) will be (AIEEE-2007)