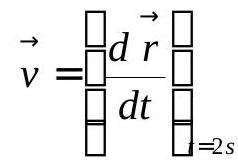269988 Two particles having position vectors \(\vec{r}_{1}=(3 \vec{i}+5 \vec{j}) m\) and \(\overrightarrow{r_{2}}=(-5 \vec{i}+3 \vec{j}) m\) are moving with velocities \(\overrightarrow{V_{1}}=(4 \hat{i}-4 \hat{j}) \mathrm{ms}^{-1}\) and \(\overrightarrow{V_{2}}=(a \hat{i}-3 \hat{j}) \mathrm{ms}^{-1}\). If they collide after 2 seconds, the value of ' \(a\) ' is
269991 A particle starts from origin at \(t=0\) with a constant velocity \(5 \hat{i} \mathrm{~ms}^{-1}\) and moves in \(\mathbf{x y}\) plane under action of a force which produces a constant acceleration of \((3 \hat{i}+2 \hat{j}) \mathrm{ms}^{-2}\). The \(\mathbf{y}\) - coordinate of the particle at the instant its \(x\) co-ordinate is \(84 \mathrm{~m}\) in \(\mathbf{m}\) is
269988 Two particles having position vectors \(\vec{r}_{1}=(3 \vec{i}+5 \vec{j}) m\) and \(\overrightarrow{r_{2}}=(-5 \vec{i}+3 \vec{j}) m\) are moving with velocities \(\overrightarrow{V_{1}}=(4 \hat{i}-4 \hat{j}) \mathrm{ms}^{-1}\) and \(\overrightarrow{V_{2}}=(a \hat{i}-3 \hat{j}) \mathrm{ms}^{-1}\). If they collide after 2 seconds, the value of ' \(a\) ' is
269991 A particle starts from origin at \(t=0\) with a constant velocity \(5 \hat{i} \mathrm{~ms}^{-1}\) and moves in \(\mathbf{x y}\) plane under action of a force which produces a constant acceleration of \((3 \hat{i}+2 \hat{j}) \mathrm{ms}^{-2}\). The \(\mathbf{y}\) - coordinate of the particle at the instant its \(x\) co-ordinate is \(84 \mathrm{~m}\) in \(\mathbf{m}\) is
269988 Two particles having position vectors \(\vec{r}_{1}=(3 \vec{i}+5 \vec{j}) m\) and \(\overrightarrow{r_{2}}=(-5 \vec{i}+3 \vec{j}) m\) are moving with velocities \(\overrightarrow{V_{1}}=(4 \hat{i}-4 \hat{j}) \mathrm{ms}^{-1}\) and \(\overrightarrow{V_{2}}=(a \hat{i}-3 \hat{j}) \mathrm{ms}^{-1}\). If they collide after 2 seconds, the value of ' \(a\) ' is
269991 A particle starts from origin at \(t=0\) with a constant velocity \(5 \hat{i} \mathrm{~ms}^{-1}\) and moves in \(\mathbf{x y}\) plane under action of a force which produces a constant acceleration of \((3 \hat{i}+2 \hat{j}) \mathrm{ms}^{-2}\). The \(\mathbf{y}\) - coordinate of the particle at the instant its \(x\) co-ordinate is \(84 \mathrm{~m}\) in \(\mathbf{m}\) is
269988 Two particles having position vectors \(\vec{r}_{1}=(3 \vec{i}+5 \vec{j}) m\) and \(\overrightarrow{r_{2}}=(-5 \vec{i}+3 \vec{j}) m\) are moving with velocities \(\overrightarrow{V_{1}}=(4 \hat{i}-4 \hat{j}) \mathrm{ms}^{-1}\) and \(\overrightarrow{V_{2}}=(a \hat{i}-3 \hat{j}) \mathrm{ms}^{-1}\). If they collide after 2 seconds, the value of ' \(a\) ' is
269991 A particle starts from origin at \(t=0\) with a constant velocity \(5 \hat{i} \mathrm{~ms}^{-1}\) and moves in \(\mathbf{x y}\) plane under action of a force which produces a constant acceleration of \((3 \hat{i}+2 \hat{j}) \mathrm{ms}^{-2}\). The \(\mathbf{y}\) - coordinate of the particle at the instant its \(x\) co-ordinate is \(84 \mathrm{~m}\) in \(\mathbf{m}\) is