269799
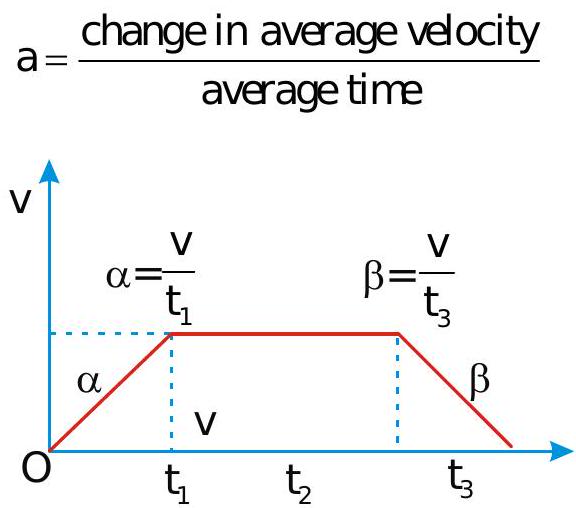
A trainstartsfrom rest and moves with uniform acceleration \(\alpha\) for sometime and acquires a velocity ' \(v\) '. It then moves with constant velocity for some time and then decelerates
at rate \(\beta\) and finally comes to rest at thenext station. If ' \(L\) ' isdistance between two stations then total time of travel is
269799
A trainstartsfrom rest and moves with uniform acceleration \(\alpha\) for sometime and acquires a velocity ' \(v\) '. It then moves with constant velocity for some time and then decelerates
at rate \(\beta\) and finally comes to rest at thenext station. If ' \(L\) ' isdistance between two stations then total time of travel is
269799
A trainstartsfrom rest and moves with uniform acceleration \(\alpha\) for sometime and acquires a velocity ' \(v\) '. It then moves with constant velocity for some time and then decelerates
at rate \(\beta\) and finally comes to rest at thenext station. If ' \(L\) ' isdistance between two stations then total time of travel is
269799
A trainstartsfrom rest and moves with uniform acceleration \(\alpha\) for sometime and acquires a velocity ' \(v\) '. It then moves with constant velocity for some time and then decelerates
at rate \(\beta\) and finally comes to rest at thenext station. If ' \(L\) ' isdistance between two stations then total time of travel is

 \(v^{2}-o^{2}=2 f s\)
\(v^{2}-o^{2}=2 f s\)