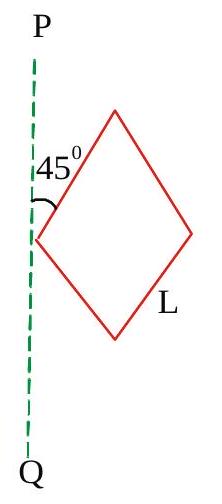
269613 A wheel having radius \(10 \mathrm{~cm}\) is coupled by a belt to another wheel of radius \(30 \mathrm{~cm}\). \(1 \mathrm{st}\) wheel increases its angular speed from rest at a uniform rate of \(1.57 \mathrm{rad} \mathrm{s}^{-2}\). The time for 2nd wheel to reach a rotational speed of 100 rev/min is...(assume that the belt does not slip)
269614
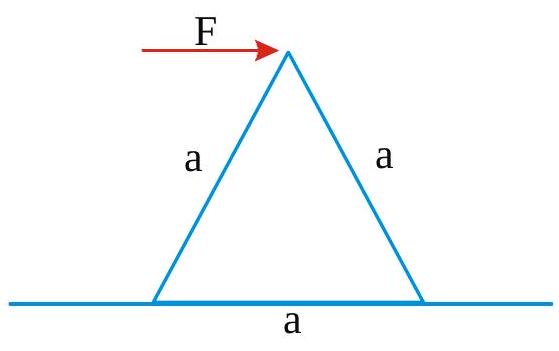
An equilateral prism of mass \(m\) rests on a rough horizontal surface with coefficient of friction \(\mu\). A horizontal force \(F\) is applied on the prism as shown. If the coefficient of friction is sufficiently high so that the prism does not slide before toppling, the minimum force required to topple the prism is
269613 A wheel having radius \(10 \mathrm{~cm}\) is coupled by a belt to another wheel of radius \(30 \mathrm{~cm}\). \(1 \mathrm{st}\) wheel increases its angular speed from rest at a uniform rate of \(1.57 \mathrm{rad} \mathrm{s}^{-2}\). The time for 2nd wheel to reach a rotational speed of 100 rev/min is...(assume that the belt does not slip)
269614
An equilateral prism of mass \(m\) rests on a rough horizontal surface with coefficient of friction \(\mu\). A horizontal force \(F\) is applied on the prism as shown. If the coefficient of friction is sufficiently high so that the prism does not slide before toppling, the minimum force required to topple the prism is

269613 A wheel having radius \(10 \mathrm{~cm}\) is coupled by a belt to another wheel of radius \(30 \mathrm{~cm}\). \(1 \mathrm{st}\) wheel increases its angular speed from rest at a uniform rate of \(1.57 \mathrm{rad} \mathrm{s}^{-2}\). The time for 2nd wheel to reach a rotational speed of 100 rev/min is...(assume that the belt does not slip)
269614
An equilateral prism of mass \(m\) rests on a rough horizontal surface with coefficient of friction \(\mu\). A horizontal force \(F\) is applied on the prism as shown. If the coefficient of friction is sufficiently high so that the prism does not slide before toppling, the minimum force required to topple the prism is

269613 A wheel having radius \(10 \mathrm{~cm}\) is coupled by a belt to another wheel of radius \(30 \mathrm{~cm}\). \(1 \mathrm{st}\) wheel increases its angular speed from rest at a uniform rate of \(1.57 \mathrm{rad} \mathrm{s}^{-2}\). The time for 2nd wheel to reach a rotational speed of 100 rev/min is...(assume that the belt does not slip)
269614
An equilateral prism of mass \(m\) rests on a rough horizontal surface with coefficient of friction \(\mu\). A horizontal force \(F\) is applied on the prism as shown. If the coefficient of friction is sufficiently high so that the prism does not slide before toppling, the minimum force required to topple the prism is