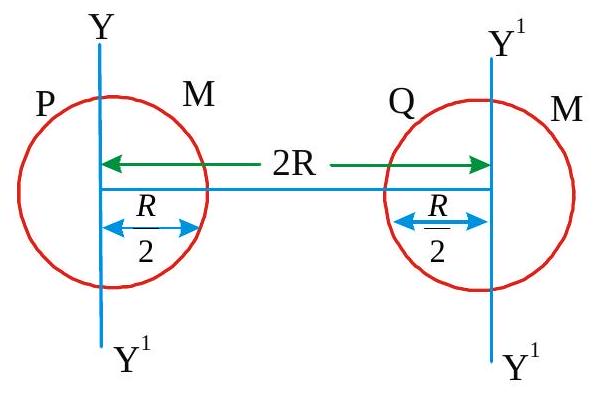
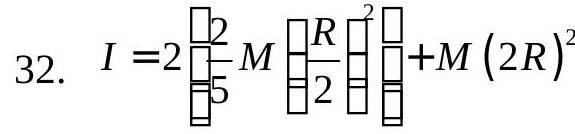269511 A wheel starting from rest is uniformly accelerated with\(\alpha=4 \mathrm{rad} / \mathrm{s}^{2}\) for \(\mathbf{1 0}\) seconds. It is then allowed to rotate uniformly for the next two seconds and is finally brought to rest in the next 10 seconds. Find the total angle rotated by the wheel.
269511 A wheel starting from rest is uniformly accelerated with\(\alpha=4 \mathrm{rad} / \mathrm{s}^{2}\) for \(\mathbf{1 0}\) seconds. It is then allowed to rotate uniformly for the next two seconds and is finally brought to rest in the next 10 seconds. Find the total angle rotated by the wheel.
269511 A wheel starting from rest is uniformly accelerated with\(\alpha=4 \mathrm{rad} / \mathrm{s}^{2}\) for \(\mathbf{1 0}\) seconds. It is then allowed to rotate uniformly for the next two seconds and is finally brought to rest in the next 10 seconds. Find the total angle rotated by the wheel.
269511 A wheel starting from rest is uniformly accelerated with\(\alpha=4 \mathrm{rad} / \mathrm{s}^{2}\) for \(\mathbf{1 0}\) seconds. It is then allowed to rotate uniformly for the next two seconds and is finally brought to rest in the next 10 seconds. Find the total angle rotated by the wheel.
269511 A wheel starting from rest is uniformly accelerated with\(\alpha=4 \mathrm{rad} / \mathrm{s}^{2}\) for \(\mathbf{1 0}\) seconds. It is then allowed to rotate uniformly for the next two seconds and is finally brought to rest in the next 10 seconds. Find the total angle rotated by the wheel.