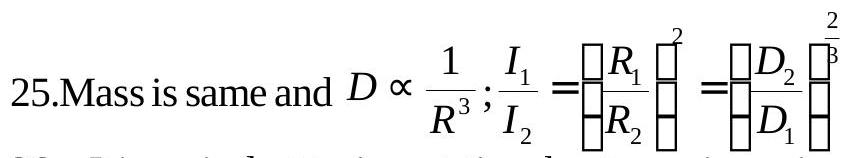269447 The moment of inertia of a solid sphere about an axis passing through itscentre is \(0.8 \mathrm{kgm}^{2}\). The moment of inertia of another solid sphere whose mass is same as mass of first sphere, but the density is 8 times density of first sphere, about an axis passing through its centre is
269447 The moment of inertia of a solid sphere about an axis passing through itscentre is \(0.8 \mathrm{kgm}^{2}\). The moment of inertia of another solid sphere whose mass is same as mass of first sphere, but the density is 8 times density of first sphere, about an axis passing through its centre is
269447 The moment of inertia of a solid sphere about an axis passing through itscentre is \(0.8 \mathrm{kgm}^{2}\). The moment of inertia of another solid sphere whose mass is same as mass of first sphere, but the density is 8 times density of first sphere, about an axis passing through its centre is
269447 The moment of inertia of a solid sphere about an axis passing through itscentre is \(0.8 \mathrm{kgm}^{2}\). The moment of inertia of another solid sphere whose mass is same as mass of first sphere, but the density is 8 times density of first sphere, about an axis passing through its centre is
269447 The moment of inertia of a solid sphere about an axis passing through itscentre is \(0.8 \mathrm{kgm}^{2}\). The moment of inertia of another solid sphere whose mass is same as mass of first sphere, but the density is 8 times density of first sphere, about an axis passing through its centre is