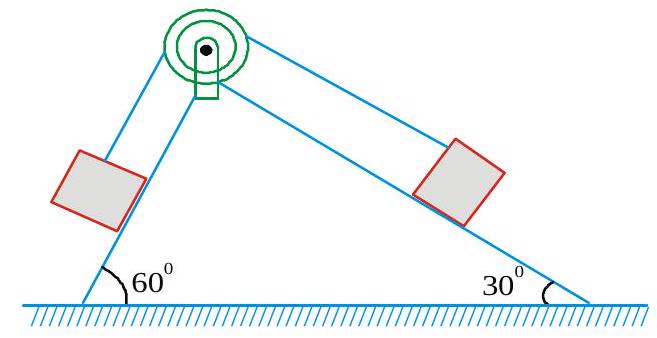
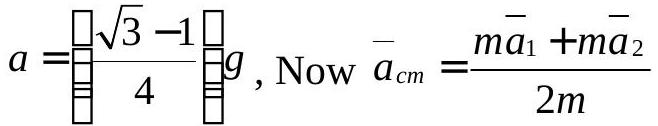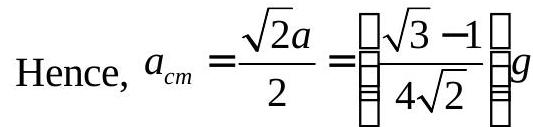269601 A body of mass ' \(m\) ' is dropped and another body of mass \(M\) is projected vertically up with speed ' \(u\) ' simultaneously from the top of a tower of height \(H\). If the body reaches the highest point before the dropped body reaches the ground, then maximum height raised by the centre of mass of the system from ground is
269603 A rope thrown over a pulley has a ladder with a man of mass \(m\) on one of its ends and a counter balancing mass \(M\) on its other end. The man climbs with a velocity \(\mathrm{v}_{r}\) relative toladder. Ignoring the masses of the pulley and the rope as well as the friction on the pulley axis, the velocity of the centre of mass of this system is :
269604 Two particles of masses \(2 \mathrm{~kg}\) and \(3 \mathrm{~kg}\) are projected horizontally in opposite directions from the top of a tower of height \(39.2 \mathrm{~m}\) with velocities \(5 \mathrm{~m} / \mathrm{s}\) and \(10 \mathrm{~m} / \mathrm{s}\) respectively. The horizontal range of the centre of mass of two particles is
269601 A body of mass ' \(m\) ' is dropped and another body of mass \(M\) is projected vertically up with speed ' \(u\) ' simultaneously from the top of a tower of height \(H\). If the body reaches the highest point before the dropped body reaches the ground, then maximum height raised by the centre of mass of the system from ground is
269603 A rope thrown over a pulley has a ladder with a man of mass \(m\) on one of its ends and a counter balancing mass \(M\) on its other end. The man climbs with a velocity \(\mathrm{v}_{r}\) relative toladder. Ignoring the masses of the pulley and the rope as well as the friction on the pulley axis, the velocity of the centre of mass of this system is :
269604 Two particles of masses \(2 \mathrm{~kg}\) and \(3 \mathrm{~kg}\) are projected horizontally in opposite directions from the top of a tower of height \(39.2 \mathrm{~m}\) with velocities \(5 \mathrm{~m} / \mathrm{s}\) and \(10 \mathrm{~m} / \mathrm{s}\) respectively. The horizontal range of the centre of mass of two particles is
269601 A body of mass ' \(m\) ' is dropped and another body of mass \(M\) is projected vertically up with speed ' \(u\) ' simultaneously from the top of a tower of height \(H\). If the body reaches the highest point before the dropped body reaches the ground, then maximum height raised by the centre of mass of the system from ground is
269603 A rope thrown over a pulley has a ladder with a man of mass \(m\) on one of its ends and a counter balancing mass \(M\) on its other end. The man climbs with a velocity \(\mathrm{v}_{r}\) relative toladder. Ignoring the masses of the pulley and the rope as well as the friction on the pulley axis, the velocity of the centre of mass of this system is :
269604 Two particles of masses \(2 \mathrm{~kg}\) and \(3 \mathrm{~kg}\) are projected horizontally in opposite directions from the top of a tower of height \(39.2 \mathrm{~m}\) with velocities \(5 \mathrm{~m} / \mathrm{s}\) and \(10 \mathrm{~m} / \mathrm{s}\) respectively. The horizontal range of the centre of mass of two particles is
269601 A body of mass ' \(m\) ' is dropped and another body of mass \(M\) is projected vertically up with speed ' \(u\) ' simultaneously from the top of a tower of height \(H\). If the body reaches the highest point before the dropped body reaches the ground, then maximum height raised by the centre of mass of the system from ground is
269603 A rope thrown over a pulley has a ladder with a man of mass \(m\) on one of its ends and a counter balancing mass \(M\) on its other end. The man climbs with a velocity \(\mathrm{v}_{r}\) relative toladder. Ignoring the masses of the pulley and the rope as well as the friction on the pulley axis, the velocity of the centre of mass of this system is :
269604 Two particles of masses \(2 \mathrm{~kg}\) and \(3 \mathrm{~kg}\) are projected horizontally in opposite directions from the top of a tower of height \(39.2 \mathrm{~m}\) with velocities \(5 \mathrm{~m} / \mathrm{s}\) and \(10 \mathrm{~m} / \mathrm{s}\) respectively. The horizontal range of the centre of mass of two particles is