269597
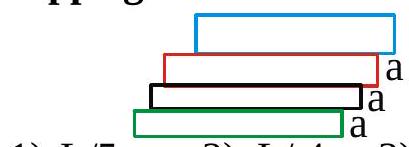
Four identical planks each of lengths ' \(L\) ' are arranged one above the other over a table as shown. Each projects a distance 'a' beyond the edge of the one that is below it. What is the maximum possible value of ' \(a\) ' for the system to be in equilibrium without tripping forward?
269598 Two masses ' \(m_{1}\) ' and ' \(m_{2}\) ' \(\left(m_{1}\lt m_{2}\right)\) are connected to the ends of a light inextensible string which passes over the surface of a smooth fixed pulley. If the system is released from rest, the acceleration of the centre of mass of the system will be ( \(g=\) acceleration due to gravity)
269597
Four identical planks each of lengths ' \(L\) ' are arranged one above the other over a table as shown. Each projects a distance 'a' beyond the edge of the one that is below it. What is the maximum possible value of ' \(a\) ' for the system to be in equilibrium without tripping forward?

269598 Two masses ' \(m_{1}\) ' and ' \(m_{2}\) ' \(\left(m_{1}\lt m_{2}\right)\) are connected to the ends of a light inextensible string which passes over the surface of a smooth fixed pulley. If the system is released from rest, the acceleration of the centre of mass of the system will be ( \(g=\) acceleration due to gravity)
269597
Four identical planks each of lengths ' \(L\) ' are arranged one above the other over a table as shown. Each projects a distance 'a' beyond the edge of the one that is below it. What is the maximum possible value of ' \(a\) ' for the system to be in equilibrium without tripping forward?

269598 Two masses ' \(m_{1}\) ' and ' \(m_{2}\) ' \(\left(m_{1}\lt m_{2}\right)\) are connected to the ends of a light inextensible string which passes over the surface of a smooth fixed pulley. If the system is released from rest, the acceleration of the centre of mass of the system will be ( \(g=\) acceleration due to gravity)
269597
Four identical planks each of lengths ' \(L\) ' are arranged one above the other over a table as shown. Each projects a distance 'a' beyond the edge of the one that is below it. What is the maximum possible value of ' \(a\) ' for the system to be in equilibrium without tripping forward?

269598 Two masses ' \(m_{1}\) ' and ' \(m_{2}\) ' \(\left(m_{1}\lt m_{2}\right)\) are connected to the ends of a light inextensible string which passes over the surface of a smooth fixed pulley. If the system is released from rest, the acceleration of the centre of mass of the system will be ( \(g=\) acceleration due to gravity)