268825 A block of mass\(10 \mathrm{~kg}\) slides down a rough slope which is inclined at \(45^{\circ}\) to the horizontal. The coefficient of sliding friction is \(\mathbf{0 . 3 0}\). When the block has to slide \(5 \mathrm{~m}\), the work done on the block by the force of friction is nearly
268872
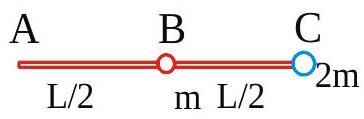
A long rod \(A B C\) of mass " \(m\) " and length " \(L\) " has two particles of masses " \(m\) " and " \(2 m\) " attached to it as shown in the figure. The system is initially in the horizontal position. The work to be done to keep it vertical with \(A\) hinged at the bottom is
268825 A block of mass\(10 \mathrm{~kg}\) slides down a rough slope which is inclined at \(45^{\circ}\) to the horizontal. The coefficient of sliding friction is \(\mathbf{0 . 3 0}\). When the block has to slide \(5 \mathrm{~m}\), the work done on the block by the force of friction is nearly
268872
A long rod \(A B C\) of mass " \(m\) " and length " \(L\) " has two particles of masses " \(m\) " and " \(2 m\) " attached to it as shown in the figure. The system is initially in the horizontal position. The work to be done to keep it vertical with \(A\) hinged at the bottom is

268825 A block of mass\(10 \mathrm{~kg}\) slides down a rough slope which is inclined at \(45^{\circ}\) to the horizontal. The coefficient of sliding friction is \(\mathbf{0 . 3 0}\). When the block has to slide \(5 \mathrm{~m}\), the work done on the block by the force of friction is nearly
268872
A long rod \(A B C\) of mass " \(m\) " and length " \(L\) " has two particles of masses " \(m\) " and " \(2 m\) " attached to it as shown in the figure. The system is initially in the horizontal position. The work to be done to keep it vertical with \(A\) hinged at the bottom is

268825 A block of mass\(10 \mathrm{~kg}\) slides down a rough slope which is inclined at \(45^{\circ}\) to the horizontal. The coefficient of sliding friction is \(\mathbf{0 . 3 0}\). When the block has to slide \(5 \mathrm{~m}\), the work done on the block by the force of friction is nearly
268872
A long rod \(A B C\) of mass " \(m\) " and length " \(L\) " has two particles of masses " \(m\) " and " \(2 m\) " attached to it as shown in the figure. The system is initially in the horizontal position. The work to be done to keep it vertical with \(A\) hinged at the bottom is

268825 A block of mass\(10 \mathrm{~kg}\) slides down a rough slope which is inclined at \(45^{\circ}\) to the horizontal. The coefficient of sliding friction is \(\mathbf{0 . 3 0}\). When the block has to slide \(5 \mathrm{~m}\), the work done on the block by the force of friction is nearly
268872
A long rod \(A B C\) of mass " \(m\) " and length " \(L\) " has two particles of masses " \(m\) " and " \(2 m\) " attached to it as shown in the figure. The system is initially in the horizontal position. The work to be done to keep it vertical with \(A\) hinged at the bottom is

