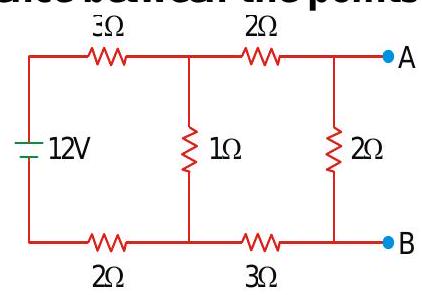
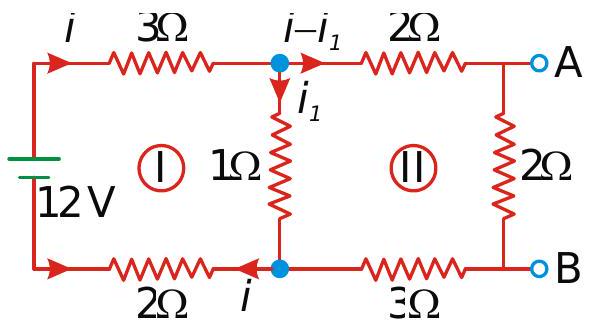
268520 Three ammeters\(P, Q\) and \(R\) with internal resistances \(r, 1.5 r\),3r respectively . \(Q\) and \(R\) parallel and this combination is in series with \(\mathrm{P}\), The whole combination concted between \(X\) and \(Y\). When the battery connected between \(X\) and \(Y\), the ratio of the readings of \(P, Q\) and \(R\) is
268523
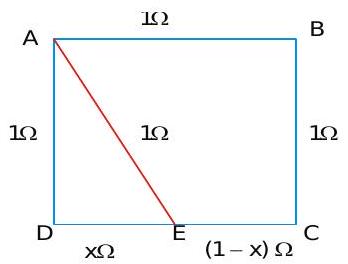
ABCD is a square where each side is a uniform wire of resistance12 . A point \(E\) lies on \(C D\) such that if a uniform wire of resistance \(1 \Omega\) is connected across AE and constant potential difference is applied across \(A\) and \(C\), then \(B\) and \(E\) are equipotential .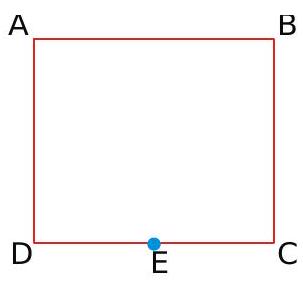
268520 Three ammeters\(P, Q\) and \(R\) with internal resistances \(r, 1.5 r\),3r respectively . \(Q\) and \(R\) parallel and this combination is in series with \(\mathrm{P}\), The whole combination concted between \(X\) and \(Y\). When the battery connected between \(X\) and \(Y\), the ratio of the readings of \(P, Q\) and \(R\) is
268523
ABCD is a square where each side is a uniform wire of resistance12 . A point \(E\) lies on \(C D\) such that if a uniform wire of resistance \(1 \Omega\) is connected across AE and constant potential difference is applied across \(A\) and \(C\), then \(B\) and \(E\) are equipotential .
268520 Three ammeters\(P, Q\) and \(R\) with internal resistances \(r, 1.5 r\),3r respectively . \(Q\) and \(R\) parallel and this combination is in series with \(\mathrm{P}\), The whole combination concted between \(X\) and \(Y\). When the battery connected between \(X\) and \(Y\), the ratio of the readings of \(P, Q\) and \(R\) is
268523
ABCD is a square where each side is a uniform wire of resistance12 . A point \(E\) lies on \(C D\) such that if a uniform wire of resistance \(1 \Omega\) is connected across AE and constant potential difference is applied across \(A\) and \(C\), then \(B\) and \(E\) are equipotential .
268520 Three ammeters\(P, Q\) and \(R\) with internal resistances \(r, 1.5 r\),3r respectively . \(Q\) and \(R\) parallel and this combination is in series with \(\mathrm{P}\), The whole combination concted between \(X\) and \(Y\). When the battery connected between \(X\) and \(Y\), the ratio of the readings of \(P, Q\) and \(R\) is
268523
ABCD is a square where each side is a uniform wire of resistance12 . A point \(E\) lies on \(C D\) such that if a uniform wire of resistance \(1 \Omega\) is connected across AE and constant potential difference is applied across \(A\) and \(C\), then \(B\) and \(E\) are equipotential .