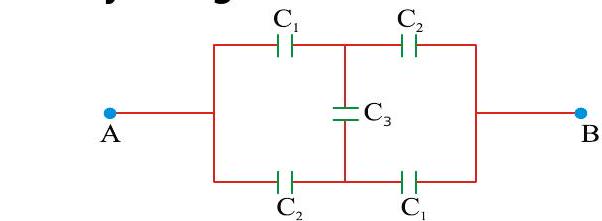
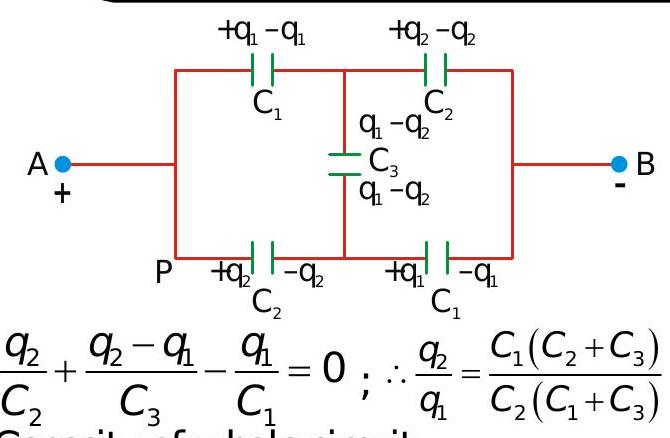
268159 A parallel plate capacitor with air as medium between the plates has a capacitance of 10\(\mu F\). The area of the capacitor is divided into two equal halves and filled with two media having dielectric constant \(K_{1}=2\) and \(K_{2}=4\). The capacitance will now be
268160 The capacity of a parallel plate condenser with air medium is\(60 \mu \mathrm{F}\) having distance of seperation \(d\). If the space between the plates is filled with two slabseach of thinckness \(d / 2\) and dielectric constants 4 and 8 , the effective capacity becomes
268159 A parallel plate capacitor with air as medium between the plates has a capacitance of 10\(\mu F\). The area of the capacitor is divided into two equal halves and filled with two media having dielectric constant \(K_{1}=2\) and \(K_{2}=4\). The capacitance will now be
268160 The capacity of a parallel plate condenser with air medium is\(60 \mu \mathrm{F}\) having distance of seperation \(d\). If the space between the plates is filled with two slabseach of thinckness \(d / 2\) and dielectric constants 4 and 8 , the effective capacity becomes
268159 A parallel plate capacitor with air as medium between the plates has a capacitance of 10\(\mu F\). The area of the capacitor is divided into two equal halves and filled with two media having dielectric constant \(K_{1}=2\) and \(K_{2}=4\). The capacitance will now be
268160 The capacity of a parallel plate condenser with air medium is\(60 \mu \mathrm{F}\) having distance of seperation \(d\). If the space between the plates is filled with two slabseach of thinckness \(d / 2\) and dielectric constants 4 and 8 , the effective capacity becomes
268159 A parallel plate capacitor with air as medium between the plates has a capacitance of 10\(\mu F\). The area of the capacitor is divided into two equal halves and filled with two media having dielectric constant \(K_{1}=2\) and \(K_{2}=4\). The capacitance will now be
268160 The capacity of a parallel plate condenser with air medium is\(60 \mu \mathrm{F}\) having distance of seperation \(d\). If the space between the plates is filled with two slabseach of thinckness \(d / 2\) and dielectric constants 4 and 8 , the effective capacity becomes