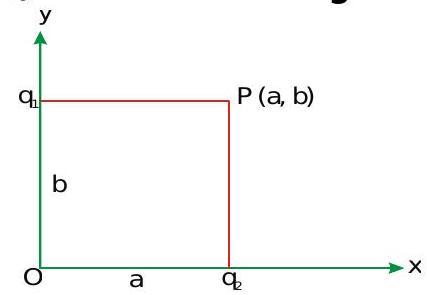
267900 Two point charges \(q_{1}=2 \mu C\) and \(q_{2}=1 \mu C\) are placed at distances \(b=1 \mathrm{~cm}\) and \(a=2 \mathrm{~cm}\) from the origin on the \(y\) and \(x\) axes as shown in figure. Theelectric field vector at point \((a, b)\) will subtend an angle \(\theta\) with thex-axis given by

1 \(\tan \theta=1\)

2 \(\tan \theta=2\)

3 \(\tan \theta=3\)

4 \(\tan \theta=4\)

267901 A non-conducting ring of radius \(0.5 \mathrm{~m}\) carries of total charge of \(1.11 \times 10^{-10} \mathrm{c}\) distributed nonuniformly on itscircumference producing an electric field \(E\) everywhere in space. The value of the integral \(\int_{I=\infty}^{I=0}-\vec{E} . d \vec{l} \quad(I=0\) being centre of the ring) in volts is

267924 A pendulum bob of mass\(m\) carrying a charge \(q\) is at rest in a uniform horizontal electric field of intensity \(E\). The tension in the thread is

267921 The breakdown electric intensity for air is\(3 \times 10^{6} \mathrm{~V} / \mathrm{m}\). The maximum charge that can be held by a sphere of radius \(1 \mathrm{~mm}\) is

267900 Two point charges \(q_{1}=2 \mu C\) and \(q_{2}=1 \mu C\) are placed at distances \(b=1 \mathrm{~cm}\) and \(a=2 \mathrm{~cm}\) from the origin on the \(y\) and \(x\) axes as shown in figure. Theelectric field vector at point \((a, b)\) will subtend an angle \(\theta\) with thex-axis given by

1 \(\tan \theta=1\)

2 \(\tan \theta=2\)

3 \(\tan \theta=3\)

4 \(\tan \theta=4\)

267901 A non-conducting ring of radius \(0.5 \mathrm{~m}\) carries of total charge of \(1.11 \times 10^{-10} \mathrm{c}\) distributed nonuniformly on itscircumference producing an electric field \(E\) everywhere in space. The value of the integral \(\int_{I=\infty}^{I=0}-\vec{E} . d \vec{l} \quad(I=0\) being centre of the ring) in volts is

267924 A pendulum bob of mass\(m\) carrying a charge \(q\) is at rest in a uniform horizontal electric field of intensity \(E\). The tension in the thread is

267921 The breakdown electric intensity for air is\(3 \times 10^{6} \mathrm{~V} / \mathrm{m}\). The maximum charge that can be held by a sphere of radius \(1 \mathrm{~mm}\) is

267900 Two point charges \(q_{1}=2 \mu C\) and \(q_{2}=1 \mu C\) are placed at distances \(b=1 \mathrm{~cm}\) and \(a=2 \mathrm{~cm}\) from the origin on the \(y\) and \(x\) axes as shown in figure. Theelectric field vector at point \((a, b)\) will subtend an angle \(\theta\) with thex-axis given by

1 \(\tan \theta=1\)

2 \(\tan \theta=2\)

3 \(\tan \theta=3\)

4 \(\tan \theta=4\)

267901 A non-conducting ring of radius \(0.5 \mathrm{~m}\) carries of total charge of \(1.11 \times 10^{-10} \mathrm{c}\) distributed nonuniformly on itscircumference producing an electric field \(E\) everywhere in space. The value of the integral \(\int_{I=\infty}^{I=0}-\vec{E} . d \vec{l} \quad(I=0\) being centre of the ring) in volts is

267924 A pendulum bob of mass\(m\) carrying a charge \(q\) is at rest in a uniform horizontal electric field of intensity \(E\). The tension in the thread is

267921 The breakdown electric intensity for air is\(3 \times 10^{6} \mathrm{~V} / \mathrm{m}\). The maximum charge that can be held by a sphere of radius \(1 \mathrm{~mm}\) is

267900 Two point charges \(q_{1}=2 \mu C\) and \(q_{2}=1 \mu C\) are placed at distances \(b=1 \mathrm{~cm}\) and \(a=2 \mathrm{~cm}\) from the origin on the \(y\) and \(x\) axes as shown in figure. Theelectric field vector at point \((a, b)\) will subtend an angle \(\theta\) with thex-axis given by

1 \(\tan \theta=1\)

2 \(\tan \theta=2\)

3 \(\tan \theta=3\)

4 \(\tan \theta=4\)

267901 A non-conducting ring of radius \(0.5 \mathrm{~m}\) carries of total charge of \(1.11 \times 10^{-10} \mathrm{c}\) distributed nonuniformly on itscircumference producing an electric field \(E\) everywhere in space. The value of the integral \(\int_{I=\infty}^{I=0}-\vec{E} . d \vec{l} \quad(I=0\) being centre of the ring) in volts is

267924 A pendulum bob of mass\(m\) carrying a charge \(q\) is at rest in a uniform horizontal electric field of intensity \(E\). The tension in the thread is

267921 The breakdown electric intensity for air is\(3 \times 10^{6} \mathrm{~V} / \mathrm{m}\). The maximum charge that can be held by a sphere of radius \(1 \mathrm{~mm}\) is