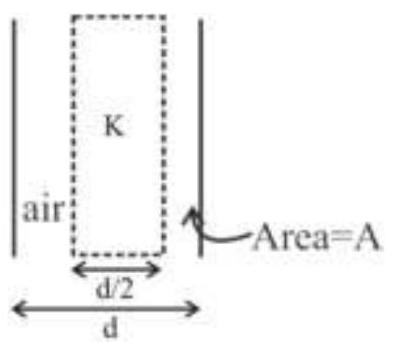
165998 The capacitance of a parallel plate capacitor becomes $\frac{4}{3}$ times its original value. If a dielectric slab of thickness $t=\frac{d}{2}$ is inserted between the plates (where, $d$ is the distance of separation between the plates). What is the dielectric constant of the slab?

165999 A parallel plate air capacitor has a capacitance C. When it is half filled with a dielectric of dielectric constant 5 , the percentage increase in the capacitance will be

166000 The capacitors $A$ and $B$ have identical geometry. A material with a dielectric constant 3 is present between the plates of $B$. The potential difference across $A$ and $B$ are respectively:

166001 A parallel plate capacitor has a capacity $C$. The separation between the plates is doubled and a dielectric medium is inserted between the plates. If the capacity is $3 \mathrm{C}$, then the dielectric constant of the medium will be

165998 The capacitance of a parallel plate capacitor becomes $\frac{4}{3}$ times its original value. If a dielectric slab of thickness $t=\frac{d}{2}$ is inserted between the plates (where, $d$ is the distance of separation between the plates). What is the dielectric constant of the slab?

165999 A parallel plate air capacitor has a capacitance C. When it is half filled with a dielectric of dielectric constant 5 , the percentage increase in the capacitance will be

166000 The capacitors $A$ and $B$ have identical geometry. A material with a dielectric constant 3 is present between the plates of $B$. The potential difference across $A$ and $B$ are respectively:

166001 A parallel plate capacitor has a capacity $C$. The separation between the plates is doubled and a dielectric medium is inserted between the plates. If the capacity is $3 \mathrm{C}$, then the dielectric constant of the medium will be

165998 The capacitance of a parallel plate capacitor becomes $\frac{4}{3}$ times its original value. If a dielectric slab of thickness $t=\frac{d}{2}$ is inserted between the plates (where, $d$ is the distance of separation between the plates). What is the dielectric constant of the slab?

165999 A parallel plate air capacitor has a capacitance C. When it is half filled with a dielectric of dielectric constant 5 , the percentage increase in the capacitance will be

166000 The capacitors $A$ and $B$ have identical geometry. A material with a dielectric constant 3 is present between the plates of $B$. The potential difference across $A$ and $B$ are respectively:

166001 A parallel plate capacitor has a capacity $C$. The separation between the plates is doubled and a dielectric medium is inserted between the plates. If the capacity is $3 \mathrm{C}$, then the dielectric constant of the medium will be

165998 The capacitance of a parallel plate capacitor becomes $\frac{4}{3}$ times its original value. If a dielectric slab of thickness $t=\frac{d}{2}$ is inserted between the plates (where, $d$ is the distance of separation between the plates). What is the dielectric constant of the slab?

165999 A parallel plate air capacitor has a capacitance C. When it is half filled with a dielectric of dielectric constant 5 , the percentage increase in the capacitance will be

166000 The capacitors $A$ and $B$ have identical geometry. A material with a dielectric constant 3 is present between the plates of $B$. The potential difference across $A$ and $B$ are respectively:

166001 A parallel plate capacitor has a capacity $C$. The separation between the plates is doubled and a dielectric medium is inserted between the plates. If the capacity is $3 \mathrm{C}$, then the dielectric constant of the medium will be