165986
A parallel plate capacitor of area $A$, plate separation $d$ and capacitance $C$ is filled with three dielectric materials having dielectric constants $k_{1}, k_{2}$ and $k_{3}$ as shown. If a single dielectric material is to be used to have the same capacitance $C$ in the capacitor, then its dielectric constant $k$ is given by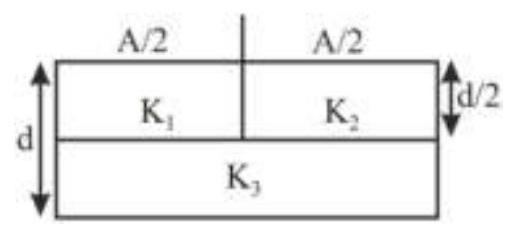
165986
A parallel plate capacitor of area $A$, plate separation $d$ and capacitance $C$ is filled with three dielectric materials having dielectric constants $k_{1}, k_{2}$ and $k_{3}$ as shown. If a single dielectric material is to be used to have the same capacitance $C$ in the capacitor, then its dielectric constant $k$ is given by
165986
A parallel plate capacitor of area $A$, plate separation $d$ and capacitance $C$ is filled with three dielectric materials having dielectric constants $k_{1}, k_{2}$ and $k_{3}$ as shown. If a single dielectric material is to be used to have the same capacitance $C$ in the capacitor, then its dielectric constant $k$ is given by
165986
A parallel plate capacitor of area $A$, plate separation $d$ and capacitance $C$ is filled with three dielectric materials having dielectric constants $k_{1}, k_{2}$ and $k_{3}$ as shown. If a single dielectric material is to be used to have the same capacitance $C$ in the capacitor, then its dielectric constant $k$ is given by
165986
A parallel plate capacitor of area $A$, plate separation $d$ and capacitance $C$ is filled with three dielectric materials having dielectric constants $k_{1}, k_{2}$ and $k_{3}$ as shown. If a single dielectric material is to be used to have the same capacitance $C$ in the capacitor, then its dielectric constant $k$ is given by