165848
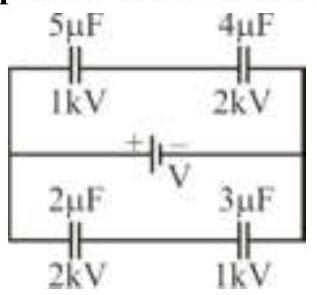
Four capacitors of capacitances $2 \mu \mathrm{F}, 3 \mu \mathrm{F}, 4 \mu \mathrm{F}$ and $x \mu F$ are connected to a battery of emf $6 \mathrm{~V}$ and of negligible internal resistance, as shown in the figure. If the ratio of the charges on $x \mu F$ and $4 \mu \mathrm{F}$ capacitances is $\frac{3}{8}$, then the value of $x$ is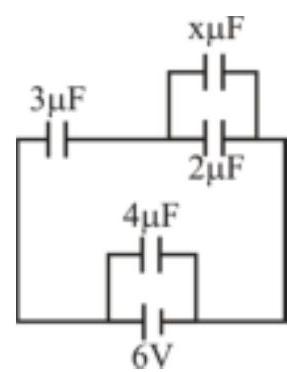
165848
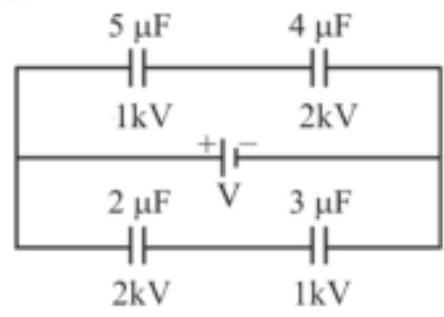
Four capacitors of capacitances $2 \mu \mathrm{F}, 3 \mu \mathrm{F}, 4 \mu \mathrm{F}$ and $x \mu F$ are connected to a battery of emf $6 \mathrm{~V}$ and of negligible internal resistance, as shown in the figure. If the ratio of the charges on $x \mu F$ and $4 \mu \mathrm{F}$ capacitances is $\frac{3}{8}$, then the value of $x$ is
165848
Four capacitors of capacitances $2 \mu \mathrm{F}, 3 \mu \mathrm{F}, 4 \mu \mathrm{F}$ and $x \mu F$ are connected to a battery of emf $6 \mathrm{~V}$ and of negligible internal resistance, as shown in the figure. If the ratio of the charges on $x \mu F$ and $4 \mu \mathrm{F}$ capacitances is $\frac{3}{8}$, then the value of $x$ is
165848
Four capacitors of capacitances $2 \mu \mathrm{F}, 3 \mu \mathrm{F}, 4 \mu \mathrm{F}$ and $x \mu F$ are connected to a battery of emf $6 \mathrm{~V}$ and of negligible internal resistance, as shown in the figure. If the ratio of the charges on $x \mu F$ and $4 \mu \mathrm{F}$ capacitances is $\frac{3}{8}$, then the value of $x$ is