165808
Two capacitors having capacitance $C_{1}$ and $C_{2}$ respectively are connected as shown in figure. Initially, capacitor $C_{1}$ is charged to a potential difference $V$ volt by a battery. The battery is then removed and the charged capacitor $C_{1}$ is now connected to uncharged capacitor $C_{2}$, by closing the switch $\mathrm{S}$. The amount of charge on the capacitor $C_{2}$ after equilibrium is: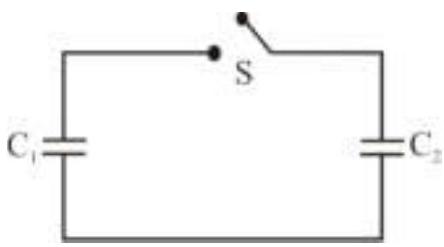
165808
Two capacitors having capacitance $C_{1}$ and $C_{2}$ respectively are connected as shown in figure. Initially, capacitor $C_{1}$ is charged to a potential difference $V$ volt by a battery. The battery is then removed and the charged capacitor $C_{1}$ is now connected to uncharged capacitor $C_{2}$, by closing the switch $\mathrm{S}$. The amount of charge on the capacitor $C_{2}$ after equilibrium is:
165808
Two capacitors having capacitance $C_{1}$ and $C_{2}$ respectively are connected as shown in figure. Initially, capacitor $C_{1}$ is charged to a potential difference $V$ volt by a battery. The battery is then removed and the charged capacitor $C_{1}$ is now connected to uncharged capacitor $C_{2}$, by closing the switch $\mathrm{S}$. The amount of charge on the capacitor $C_{2}$ after equilibrium is:
165808
Two capacitors having capacitance $C_{1}$ and $C_{2}$ respectively are connected as shown in figure. Initially, capacitor $C_{1}$ is charged to a potential difference $V$ volt by a battery. The battery is then removed and the charged capacitor $C_{1}$ is now connected to uncharged capacitor $C_{2}$, by closing the switch $\mathrm{S}$. The amount of charge on the capacitor $C_{2}$ after equilibrium is:
165808
Two capacitors having capacitance $C_{1}$ and $C_{2}$ respectively are connected as shown in figure. Initially, capacitor $C_{1}$ is charged to a potential difference $V$ volt by a battery. The battery is then removed and the charged capacitor $C_{1}$ is now connected to uncharged capacitor $C_{2}$, by closing the switch $\mathrm{S}$. The amount of charge on the capacitor $C_{2}$ after equilibrium is: