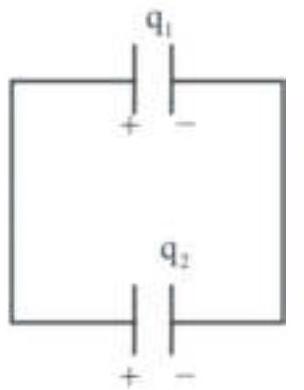
165801 A capacitor of capacity $10 \mu \mathrm{F}$ is charged to $40 \mathrm{~V}$ and a second capacitor of capacity $15 \mu \mathrm{F}$ is charged to $30 \mathrm{~V}$. If they are connected in parallel the amount of charge that flows from the smaller capacitor to higher capacitor in $\mu \mathrm{C}$ is:
165801 A capacitor of capacity $10 \mu \mathrm{F}$ is charged to $40 \mathrm{~V}$ and a second capacitor of capacity $15 \mu \mathrm{F}$ is charged to $30 \mathrm{~V}$. If they are connected in parallel the amount of charge that flows from the smaller capacitor to higher capacitor in $\mu \mathrm{C}$ is:
165801 A capacitor of capacity $10 \mu \mathrm{F}$ is charged to $40 \mathrm{~V}$ and a second capacitor of capacity $15 \mu \mathrm{F}$ is charged to $30 \mathrm{~V}$. If they are connected in parallel the amount of charge that flows from the smaller capacitor to higher capacitor in $\mu \mathrm{C}$ is:
165801 A capacitor of capacity $10 \mu \mathrm{F}$ is charged to $40 \mathrm{~V}$ and a second capacitor of capacity $15 \mu \mathrm{F}$ is charged to $30 \mathrm{~V}$. If they are connected in parallel the amount of charge that flows from the smaller capacitor to higher capacitor in $\mu \mathrm{C}$ is: