165697
Two identical capacitors $C_{1}$ and $C_{2}$ of equal capacitance are connected as shown in the circuit. Terminals a and $b$ of the key $k$ are connected to charge capacitor $C_{1}$ using battery of emf $V$ volt. Now, disconnecting a and $b$ the terminals $b$ and $c$ are connected. Due to this, what will be the percentage loss of energy?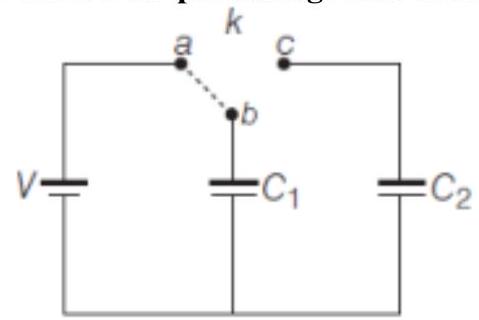
165697
Two identical capacitors $C_{1}$ and $C_{2}$ of equal capacitance are connected as shown in the circuit. Terminals a and $b$ of the key $k$ are connected to charge capacitor $C_{1}$ using battery of emf $V$ volt. Now, disconnecting a and $b$ the terminals $b$ and $c$ are connected. Due to this, what will be the percentage loss of energy?
165697
Two identical capacitors $C_{1}$ and $C_{2}$ of equal capacitance are connected as shown in the circuit. Terminals a and $b$ of the key $k$ are connected to charge capacitor $C_{1}$ using battery of emf $V$ volt. Now, disconnecting a and $b$ the terminals $b$ and $c$ are connected. Due to this, what will be the percentage loss of energy?
165697
Two identical capacitors $C_{1}$ and $C_{2}$ of equal capacitance are connected as shown in the circuit. Terminals a and $b$ of the key $k$ are connected to charge capacitor $C_{1}$ using battery of emf $V$ volt. Now, disconnecting a and $b$ the terminals $b$ and $c$ are connected. Due to this, what will be the percentage loss of energy?