165691
Two identical condensers are joined as shown in the figure. When the switch $S$ is closed, the total energy of the system is $U_{1}$. If the switch is opened and both the condensers are filled with a dielectric of dielectric constant 3 . then the energy of the system becomes $U_{2}$.
The value of $\frac{U_{1}}{U_{2}}$ is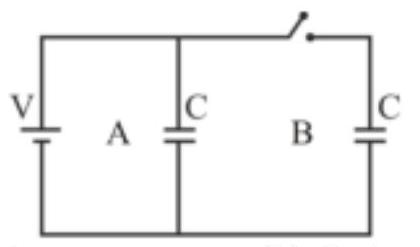
165691
Two identical condensers are joined as shown in the figure. When the switch $S$ is closed, the total energy of the system is $U_{1}$. If the switch is opened and both the condensers are filled with a dielectric of dielectric constant 3 . then the energy of the system becomes $U_{2}$.
The value of $\frac{U_{1}}{U_{2}}$ is
165691
Two identical condensers are joined as shown in the figure. When the switch $S$ is closed, the total energy of the system is $U_{1}$. If the switch is opened and both the condensers are filled with a dielectric of dielectric constant 3 . then the energy of the system becomes $U_{2}$.
The value of $\frac{U_{1}}{U_{2}}$ is
165691
Two identical condensers are joined as shown in the figure. When the switch $S$ is closed, the total energy of the system is $U_{1}$. If the switch is opened and both the condensers are filled with a dielectric of dielectric constant 3 . then the energy of the system becomes $U_{2}$.
The value of $\frac{U_{1}}{U_{2}}$ is