142191
The following graph represents the variation of photocurrent with anode potential for a metal surface. Here, $I_{1}, I_{2}$ and $I_{3}$ represents intensities and $\gamma_{1}, \gamma_{2}, \gamma_{3}$ represent frequency for curves 1,2 and 3 respectively, then :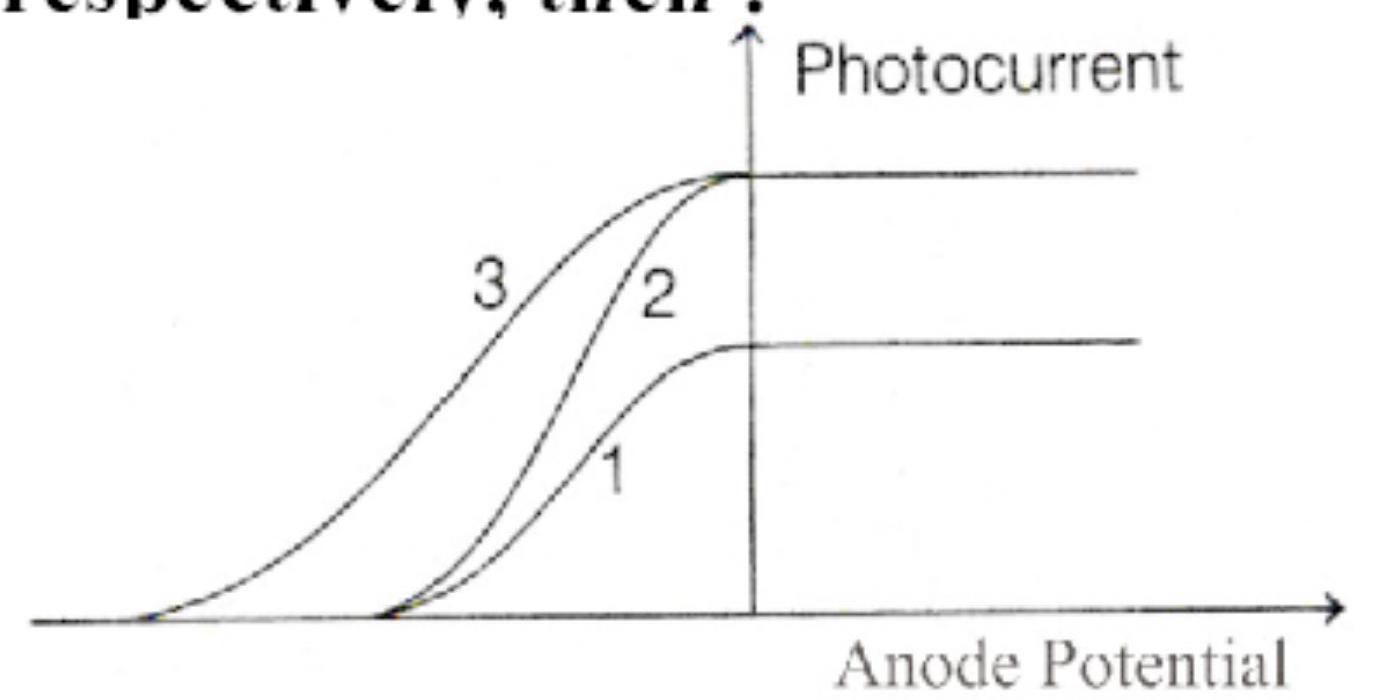
142192
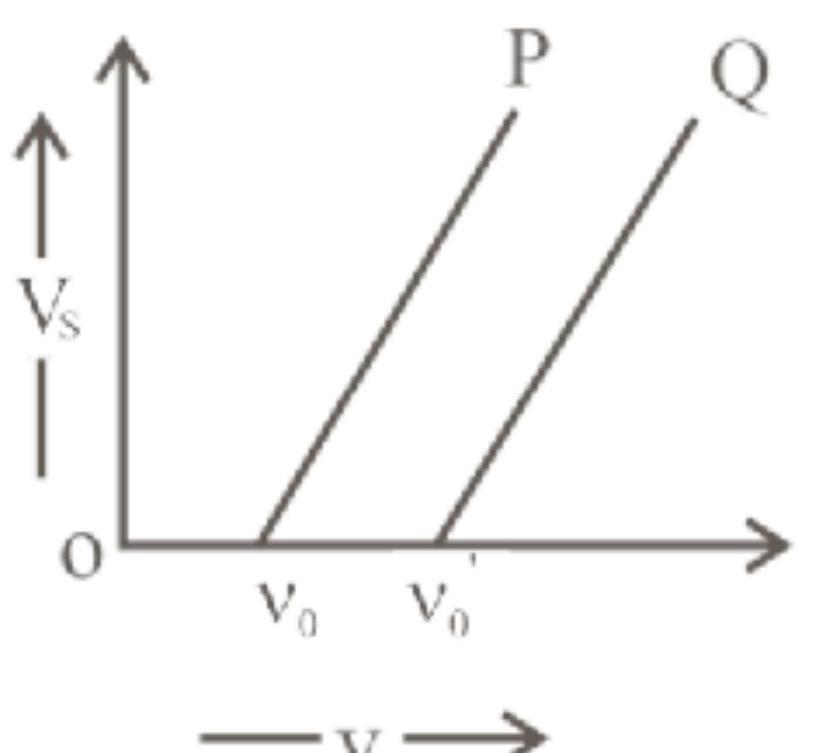
The graph of stopping potential $\left(V_{s}\right)$ against frequency $(v)$ of incident radiation is plotted for two different metals ' $P$ ' and ' $Q$ ' as shown in the graph. $\phi_{\mathrm{p}}$ and $\phi_{\mathrm{Q}}$ are work functions of $\mathrm{P}$ and $Q$ respectively, then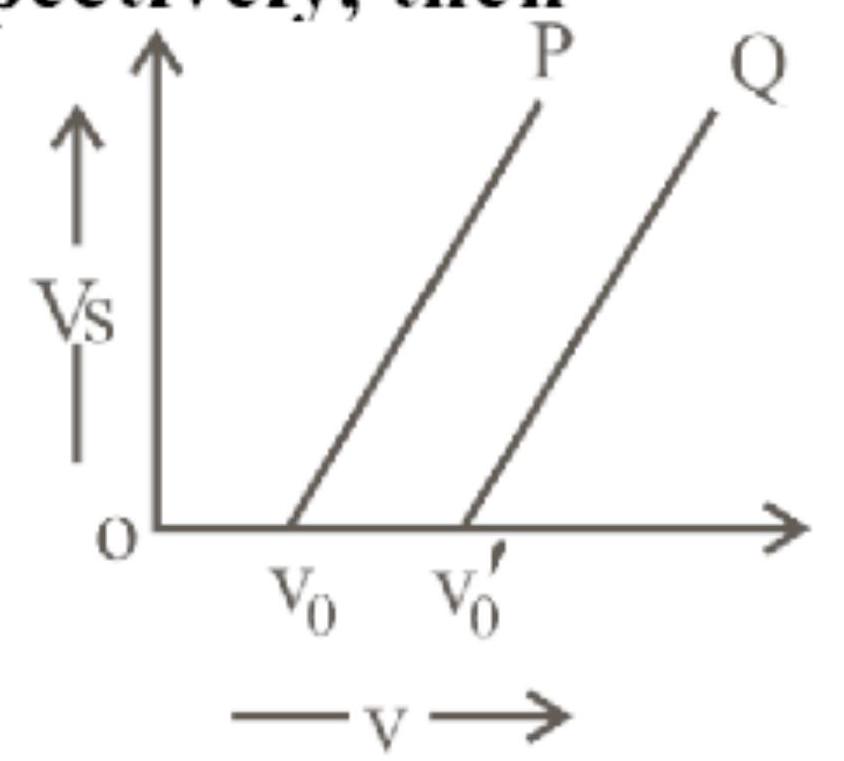
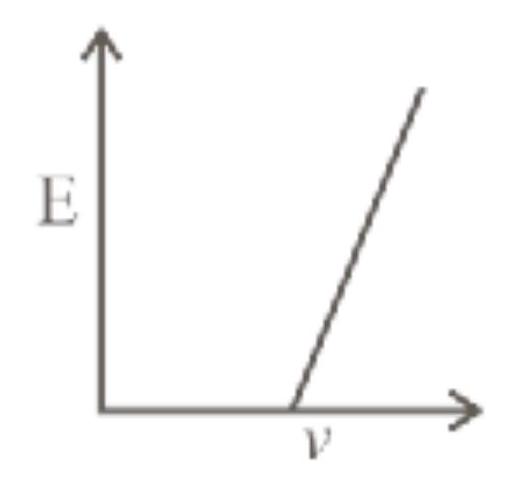
142194 A metal surface having work function ' $w_{0}$ ' emits photoelectrons when photons of energy ' $E$ ' are incident on it. The electron enters the uniform magnetic field $(B)$ in perpendicular direction and moves in circular path of radius ' $r$ '. Then ' $r$ ' is equal to ( $m$ and e be the mass and charge of electron respectively).
142191
The following graph represents the variation of photocurrent with anode potential for a metal surface. Here, $I_{1}, I_{2}$ and $I_{3}$ represents intensities and $\gamma_{1}, \gamma_{2}, \gamma_{3}$ represent frequency for curves 1,2 and 3 respectively, then :
142192
The graph of stopping potential $\left(V_{s}\right)$ against frequency $(v)$ of incident radiation is plotted for two different metals ' $P$ ' and ' $Q$ ' as shown in the graph. $\phi_{\mathrm{p}}$ and $\phi_{\mathrm{Q}}$ are work functions of $\mathrm{P}$ and $Q$ respectively, then
142194 A metal surface having work function ' $w_{0}$ ' emits photoelectrons when photons of energy ' $E$ ' are incident on it. The electron enters the uniform magnetic field $(B)$ in perpendicular direction and moves in circular path of radius ' $r$ '. Then ' $r$ ' is equal to ( $m$ and e be the mass and charge of electron respectively).
142191
The following graph represents the variation of photocurrent with anode potential for a metal surface. Here, $I_{1}, I_{2}$ and $I_{3}$ represents intensities and $\gamma_{1}, \gamma_{2}, \gamma_{3}$ represent frequency for curves 1,2 and 3 respectively, then :
142192
The graph of stopping potential $\left(V_{s}\right)$ against frequency $(v)$ of incident radiation is plotted for two different metals ' $P$ ' and ' $Q$ ' as shown in the graph. $\phi_{\mathrm{p}}$ and $\phi_{\mathrm{Q}}$ are work functions of $\mathrm{P}$ and $Q$ respectively, then
142194 A metal surface having work function ' $w_{0}$ ' emits photoelectrons when photons of energy ' $E$ ' are incident on it. The electron enters the uniform magnetic field $(B)$ in perpendicular direction and moves in circular path of radius ' $r$ '. Then ' $r$ ' is equal to ( $m$ and e be the mass and charge of electron respectively).
142191
The following graph represents the variation of photocurrent with anode potential for a metal surface. Here, $I_{1}, I_{2}$ and $I_{3}$ represents intensities and $\gamma_{1}, \gamma_{2}, \gamma_{3}$ represent frequency for curves 1,2 and 3 respectively, then :
142192
The graph of stopping potential $\left(V_{s}\right)$ against frequency $(v)$ of incident radiation is plotted for two different metals ' $P$ ' and ' $Q$ ' as shown in the graph. $\phi_{\mathrm{p}}$ and $\phi_{\mathrm{Q}}$ are work functions of $\mathrm{P}$ and $Q$ respectively, then
142194 A metal surface having work function ' $w_{0}$ ' emits photoelectrons when photons of energy ' $E$ ' are incident on it. The electron enters the uniform magnetic field $(B)$ in perpendicular direction and moves in circular path of radius ' $r$ '. Then ' $r$ ' is equal to ( $m$ and e be the mass and charge of electron respectively).