142003
The variation of stopping potential for metals $A, B, C$ and $D$ with frequency of incident radiation is as shown in the figure. For which metal, stopping potential is higher for lower values of threshold frequency (v)? [The frequency of incident radiation, ' $v$ ' is same.]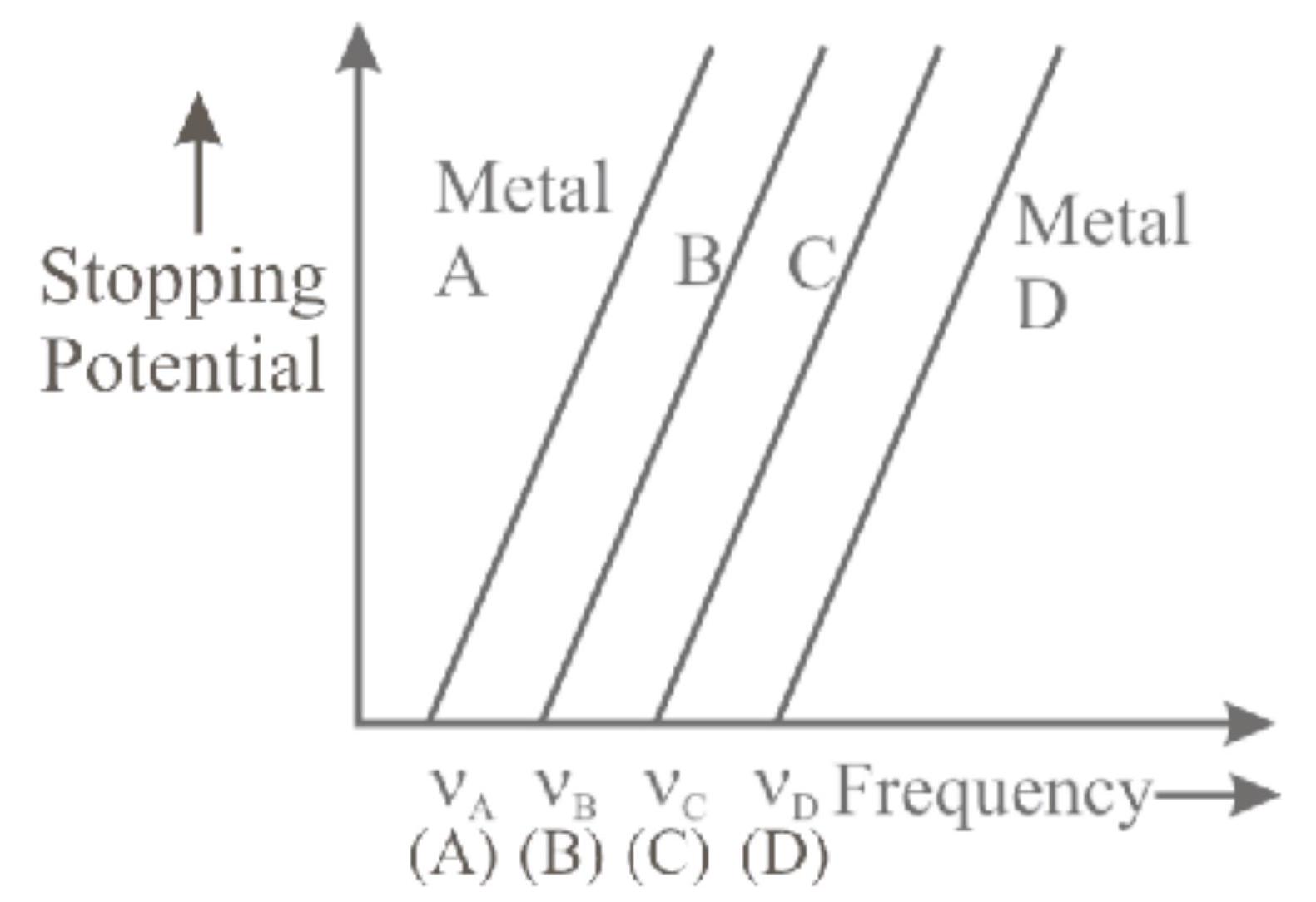
142004
If the maximum kinetic energy of emitted electrons in photoelectric effect is $3.2 \times 10^{-19} \mathrm{~J}$ and the work function for metal is $6.63 \times 10^{-19}$ $\mathrm{J}$, then stopping potential and threshold wavelength respectively are [Planck's constant $\left.\mathrm{h}=6.63 \times 10^{-34} \mathrm{~J} . \mathrm{s}\right]\left[\right.$ Velocity of light $\mathrm{c}=3 \times 10^{8}$ $\frac{\mathbf{m}}{\mathbf{s}}$ ]
[charge on electron $=1.6 \times 10^{-19} \mathrm{C}$ ]
142007 When a surface $1 \mathrm{~cm}$ thick is illuminated by light of wavelength ' $\lambda$ ', the stopping potential is ' $V_{0}$ '. When the same surface is illuminated by light of wavelength ' $3 \lambda$ ', the stopping potential is $\frac{V_{0}}{6}$. The threshold wavelength for the metallic surface is
142003
The variation of stopping potential for metals $A, B, C$ and $D$ with frequency of incident radiation is as shown in the figure. For which metal, stopping potential is higher for lower values of threshold frequency (v)? [The frequency of incident radiation, ' $v$ ' is same.]
142004
If the maximum kinetic energy of emitted electrons in photoelectric effect is $3.2 \times 10^{-19} \mathrm{~J}$ and the work function for metal is $6.63 \times 10^{-19}$ $\mathrm{J}$, then stopping potential and threshold wavelength respectively are [Planck's constant $\left.\mathrm{h}=6.63 \times 10^{-34} \mathrm{~J} . \mathrm{s}\right]\left[\right.$ Velocity of light $\mathrm{c}=3 \times 10^{8}$ $\frac{\mathbf{m}}{\mathbf{s}}$ ]
[charge on electron $=1.6 \times 10^{-19} \mathrm{C}$ ]
142007 When a surface $1 \mathrm{~cm}$ thick is illuminated by light of wavelength ' $\lambda$ ', the stopping potential is ' $V_{0}$ '. When the same surface is illuminated by light of wavelength ' $3 \lambda$ ', the stopping potential is $\frac{V_{0}}{6}$. The threshold wavelength for the metallic surface is
142003
The variation of stopping potential for metals $A, B, C$ and $D$ with frequency of incident radiation is as shown in the figure. For which metal, stopping potential is higher for lower values of threshold frequency (v)? [The frequency of incident radiation, ' $v$ ' is same.]
142004
If the maximum kinetic energy of emitted electrons in photoelectric effect is $3.2 \times 10^{-19} \mathrm{~J}$ and the work function for metal is $6.63 \times 10^{-19}$ $\mathrm{J}$, then stopping potential and threshold wavelength respectively are [Planck's constant $\left.\mathrm{h}=6.63 \times 10^{-34} \mathrm{~J} . \mathrm{s}\right]\left[\right.$ Velocity of light $\mathrm{c}=3 \times 10^{8}$ $\frac{\mathbf{m}}{\mathbf{s}}$ ]
[charge on electron $=1.6 \times 10^{-19} \mathrm{C}$ ]
142007 When a surface $1 \mathrm{~cm}$ thick is illuminated by light of wavelength ' $\lambda$ ', the stopping potential is ' $V_{0}$ '. When the same surface is illuminated by light of wavelength ' $3 \lambda$ ', the stopping potential is $\frac{V_{0}}{6}$. The threshold wavelength for the metallic surface is
142003
The variation of stopping potential for metals $A, B, C$ and $D$ with frequency of incident radiation is as shown in the figure. For which metal, stopping potential is higher for lower values of threshold frequency (v)? [The frequency of incident radiation, ' $v$ ' is same.]
142004
If the maximum kinetic energy of emitted electrons in photoelectric effect is $3.2 \times 10^{-19} \mathrm{~J}$ and the work function for metal is $6.63 \times 10^{-19}$ $\mathrm{J}$, then stopping potential and threshold wavelength respectively are [Planck's constant $\left.\mathrm{h}=6.63 \times 10^{-34} \mathrm{~J} . \mathrm{s}\right]\left[\right.$ Velocity of light $\mathrm{c}=3 \times 10^{8}$ $\frac{\mathbf{m}}{\mathbf{s}}$ ]
[charge on electron $=1.6 \times 10^{-19} \mathrm{C}$ ]
142007 When a surface $1 \mathrm{~cm}$ thick is illuminated by light of wavelength ' $\lambda$ ', the stopping potential is ' $V_{0}$ '. When the same surface is illuminated by light of wavelength ' $3 \lambda$ ', the stopping potential is $\frac{V_{0}}{6}$. The threshold wavelength for the metallic surface is