90695
DIRECTION: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
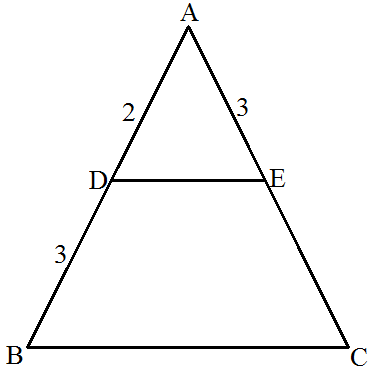
Assertion: D and E are points on the sides AB and AC respectively of a \( \triangle\text{ABC} \) such that DE||BC then the value of x is 11, when AD = 4cm, DB = (x - 4)cm, AE = 8cm and EC = (3x - 19)cm. Reason : If a line divides any two sides of a triangle in the same ratio then it is parallel.
Reason: If a line divides any two sides of a triangle in the same ratio then it is parallel to the third side.
90695
DIRECTION: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion: D and E are points on the sides AB and AC respectively of a \( \triangle\text{ABC} \) such that DE||BC then the value of x is 11, when AD = 4cm, DB = (x - 4)cm, AE = 8cm and EC = (3x - 19)cm. Reason : If a line divides any two sides of a triangle in the same ratio then it is parallel.
Reason: If a line divides any two sides of a triangle in the same ratio then it is parallel to the third side.
90695
DIRECTION: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion: D and E are points on the sides AB and AC respectively of a \( \triangle\text{ABC} \) such that DE||BC then the value of x is 11, when AD = 4cm, DB = (x - 4)cm, AE = 8cm and EC = (3x - 19)cm. Reason : If a line divides any two sides of a triangle in the same ratio then it is parallel.
Reason: If a line divides any two sides of a triangle in the same ratio then it is parallel to the third side.
90695
DIRECTION: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion: D and E are points on the sides AB and AC respectively of a \( \triangle\text{ABC} \) such that DE||BC then the value of x is 11, when AD = 4cm, DB = (x - 4)cm, AE = 8cm and EC = (3x - 19)cm. Reason : If a line divides any two sides of a triangle in the same ratio then it is parallel.
Reason: If a line divides any two sides of a triangle in the same ratio then it is parallel to the third side.
.png)
