90676 DIRECTION: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
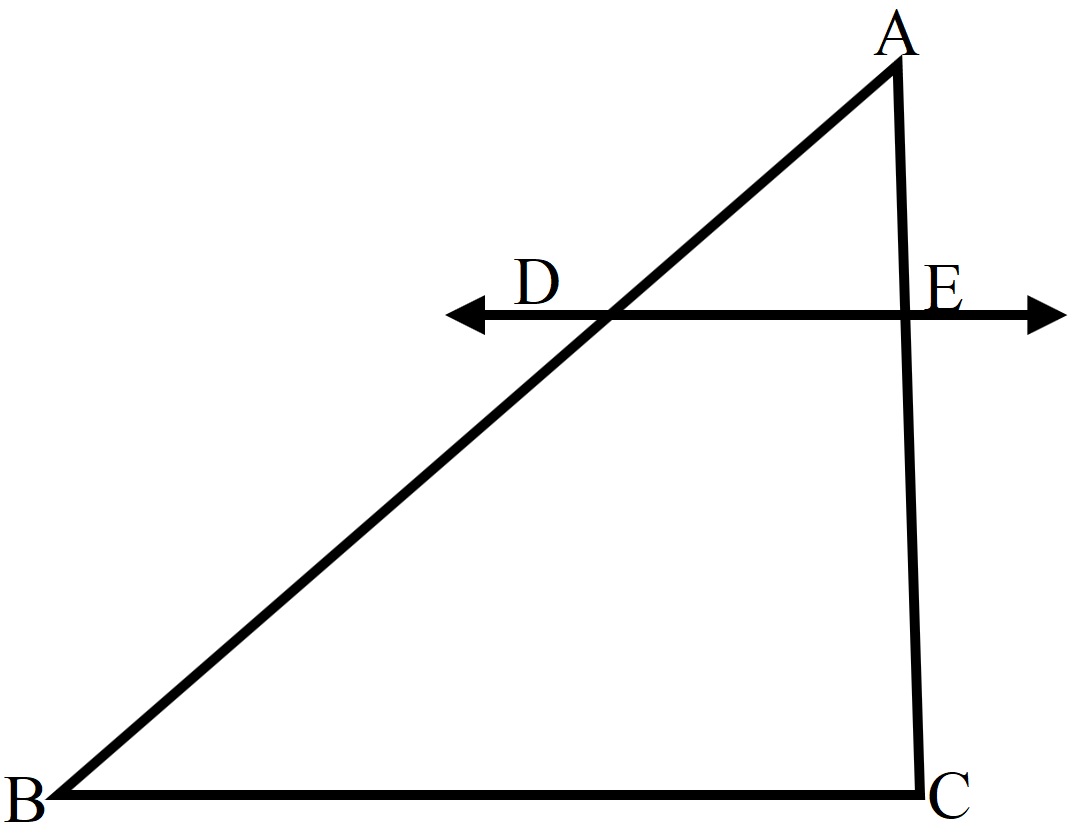
Assertion: If a line intersects sides AB and AC of a \( △ \) ABC at D and E respectively and is parallel to BC, then \(\frac{\text{AD}}{\text{AB}}=\frac{\text{AE}}{\text{AC}} \)
Reason: If a line is parallel to one side of a triangle then it divides the other two sides in the same ratio.

90677 In \(\triangle\text{ABC}\sim\triangle\text{DEF} \) and the perimeters of \(\triangle\text{ABC} \) and \(\triangle\text{DEF} \) are 30cm and 18cm respectively. If BC = 9cm then EF =?

90678 In an equilateral triangle ABC if \(\text{AD}\perp\text{BC}, \) then AD\(^{2}\) =

90679 It is given that \(\triangle\text{ABC}\sim\text{PQR} \), with \(\frac{\text{BC}}{\text{QR}}=\frac{1}{4} \) then, ar\(\frac{\text{ar}\text({\triangle{\text{PRQ}}})}{\text{ar}\text({\text{ABC}})} \) is equal to:

90676 DIRECTION: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion: If a line intersects sides AB and AC of a \( △ \) ABC at D and E respectively and is parallel to BC, then \(\frac{\text{AD}}{\text{AB}}=\frac{\text{AE}}{\text{AC}} \)
Reason: If a line is parallel to one side of a triangle then it divides the other two sides in the same ratio.

90677 In \(\triangle\text{ABC}\sim\triangle\text{DEF} \) and the perimeters of \(\triangle\text{ABC} \) and \(\triangle\text{DEF} \) are 30cm and 18cm respectively. If BC = 9cm then EF =?

90678 In an equilateral triangle ABC if \(\text{AD}\perp\text{BC}, \) then AD\(^{2}\) =

90679 It is given that \(\triangle\text{ABC}\sim\text{PQR} \), with \(\frac{\text{BC}}{\text{QR}}=\frac{1}{4} \) then, ar\(\frac{\text{ar}\text({\triangle{\text{PRQ}}})}{\text{ar}\text({\text{ABC}})} \) is equal to:

90676 DIRECTION: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion: If a line intersects sides AB and AC of a \( △ \) ABC at D and E respectively and is parallel to BC, then \(\frac{\text{AD}}{\text{AB}}=\frac{\text{AE}}{\text{AC}} \)
Reason: If a line is parallel to one side of a triangle then it divides the other two sides in the same ratio.

90677 In \(\triangle\text{ABC}\sim\triangle\text{DEF} \) and the perimeters of \(\triangle\text{ABC} \) and \(\triangle\text{DEF} \) are 30cm and 18cm respectively. If BC = 9cm then EF =?

90678 In an equilateral triangle ABC if \(\text{AD}\perp\text{BC}, \) then AD\(^{2}\) =

90679 It is given that \(\triangle\text{ABC}\sim\text{PQR} \), with \(\frac{\text{BC}}{\text{QR}}=\frac{1}{4} \) then, ar\(\frac{\text{ar}\text({\triangle{\text{PRQ}}})}{\text{ar}\text({\text{ABC}})} \) is equal to:

90676 DIRECTION: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
Assertion: If a line intersects sides AB and AC of a \( △ \) ABC at D and E respectively and is parallel to BC, then \(\frac{\text{AD}}{\text{AB}}=\frac{\text{AE}}{\text{AC}} \)
Reason: If a line is parallel to one side of a triangle then it divides the other two sides in the same ratio.

90677 In \(\triangle\text{ABC}\sim\triangle\text{DEF} \) and the perimeters of \(\triangle\text{ABC} \) and \(\triangle\text{DEF} \) are 30cm and 18cm respectively. If BC = 9cm then EF =?

90678 In an equilateral triangle ABC if \(\text{AD}\perp\text{BC}, \) then AD\(^{2}\) =

90679 It is given that \(\triangle\text{ABC}\sim\text{PQR} \), with \(\frac{\text{BC}}{\text{QR}}=\frac{1}{4} \) then, ar\(\frac{\text{ar}\text({\triangle{\text{PRQ}}})}{\text{ar}\text({\text{ABC}})} \) is equal to: