138290 The weight of a body at the surface of earth is $18 \mathrm{~N}$. The weight of the body at an altitude of $3200 \mathrm{~km}$ above the earth's surface is (given, radius of earth $R_{e}=6400 \mathrm{~km}$ )

138292 T is the time period of simple pendulum on the earth's surface. Its time period becomes $x \mathbf{T}$ when taken to a height $R$ (equal to earth's radius) above the earth's surface. Then, the value of $x$ will be

138293 At a certain depth " $d$ " below surface of earth, value of acceleration due to gravity becomes four times that of its value at a height $3 R$ above earth surface. Where $R$ is Radius of earth (Take $R=6400 \mathrm{Km}$ ). The depth $d$ is equal to

138294 Two planets $A$ and $B$ have the same average density. Their radii $R_{A}$ and $R_{B}$ are such that $R_{A}: R_{B}=3: 1$. If $g_{A}$ and $g_{B}$ are the acceleration due to gravity at the surfaces of the planets, the $g_{A}: g_{B}$ equals

138295 A uniform rod of length of $1 \mathrm{~m}$ and mass of 2 $\mathrm{kg}$ is attached to a side support at $\mathrm{O}$ as shown in the figure. The rod is at equilibrium due to upward force $T$ acting at $P$. Assume the acceleration due to gravity as $10 \mathrm{~m} / \mathrm{s}^{2}$. The value of $T$ is

138290 The weight of a body at the surface of earth is $18 \mathrm{~N}$. The weight of the body at an altitude of $3200 \mathrm{~km}$ above the earth's surface is (given, radius of earth $R_{e}=6400 \mathrm{~km}$ )

138292 T is the time period of simple pendulum on the earth's surface. Its time period becomes $x \mathbf{T}$ when taken to a height $R$ (equal to earth's radius) above the earth's surface. Then, the value of $x$ will be

138293 At a certain depth " $d$ " below surface of earth, value of acceleration due to gravity becomes four times that of its value at a height $3 R$ above earth surface. Where $R$ is Radius of earth (Take $R=6400 \mathrm{Km}$ ). The depth $d$ is equal to

138294 Two planets $A$ and $B$ have the same average density. Their radii $R_{A}$ and $R_{B}$ are such that $R_{A}: R_{B}=3: 1$. If $g_{A}$ and $g_{B}$ are the acceleration due to gravity at the surfaces of the planets, the $g_{A}: g_{B}$ equals

138295 A uniform rod of length of $1 \mathrm{~m}$ and mass of 2 $\mathrm{kg}$ is attached to a side support at $\mathrm{O}$ as shown in the figure. The rod is at equilibrium due to upward force $T$ acting at $P$. Assume the acceleration due to gravity as $10 \mathrm{~m} / \mathrm{s}^{2}$. The value of $T$ is

138290 The weight of a body at the surface of earth is $18 \mathrm{~N}$. The weight of the body at an altitude of $3200 \mathrm{~km}$ above the earth's surface is (given, radius of earth $R_{e}=6400 \mathrm{~km}$ )

138292 T is the time period of simple pendulum on the earth's surface. Its time period becomes $x \mathbf{T}$ when taken to a height $R$ (equal to earth's radius) above the earth's surface. Then, the value of $x$ will be

138293 At a certain depth " $d$ " below surface of earth, value of acceleration due to gravity becomes four times that of its value at a height $3 R$ above earth surface. Where $R$ is Radius of earth (Take $R=6400 \mathrm{Km}$ ). The depth $d$ is equal to

138294 Two planets $A$ and $B$ have the same average density. Their radii $R_{A}$ and $R_{B}$ are such that $R_{A}: R_{B}=3: 1$. If $g_{A}$ and $g_{B}$ are the acceleration due to gravity at the surfaces of the planets, the $g_{A}: g_{B}$ equals

138295 A uniform rod of length of $1 \mathrm{~m}$ and mass of 2 $\mathrm{kg}$ is attached to a side support at $\mathrm{O}$ as shown in the figure. The rod is at equilibrium due to upward force $T$ acting at $P$. Assume the acceleration due to gravity as $10 \mathrm{~m} / \mathrm{s}^{2}$. The value of $T$ is

138290 The weight of a body at the surface of earth is $18 \mathrm{~N}$. The weight of the body at an altitude of $3200 \mathrm{~km}$ above the earth's surface is (given, radius of earth $R_{e}=6400 \mathrm{~km}$ )

138292 T is the time period of simple pendulum on the earth's surface. Its time period becomes $x \mathbf{T}$ when taken to a height $R$ (equal to earth's radius) above the earth's surface. Then, the value of $x$ will be

138293 At a certain depth " $d$ " below surface of earth, value of acceleration due to gravity becomes four times that of its value at a height $3 R$ above earth surface. Where $R$ is Radius of earth (Take $R=6400 \mathrm{Km}$ ). The depth $d$ is equal to

138294 Two planets $A$ and $B$ have the same average density. Their radii $R_{A}$ and $R_{B}$ are such that $R_{A}: R_{B}=3: 1$. If $g_{A}$ and $g_{B}$ are the acceleration due to gravity at the surfaces of the planets, the $g_{A}: g_{B}$ equals

138295 A uniform rod of length of $1 \mathrm{~m}$ and mass of 2 $\mathrm{kg}$ is attached to a side support at $\mathrm{O}$ as shown in the figure. The rod is at equilibrium due to upward force $T$ acting at $P$. Assume the acceleration due to gravity as $10 \mathrm{~m} / \mathrm{s}^{2}$. The value of $T$ is

138290 The weight of a body at the surface of earth is $18 \mathrm{~N}$. The weight of the body at an altitude of $3200 \mathrm{~km}$ above the earth's surface is (given, radius of earth $R_{e}=6400 \mathrm{~km}$ )

138292 T is the time period of simple pendulum on the earth's surface. Its time period becomes $x \mathbf{T}$ when taken to a height $R$ (equal to earth's radius) above the earth's surface. Then, the value of $x$ will be

138293 At a certain depth " $d$ " below surface of earth, value of acceleration due to gravity becomes four times that of its value at a height $3 R$ above earth surface. Where $R$ is Radius of earth (Take $R=6400 \mathrm{Km}$ ). The depth $d$ is equal to

138294 Two planets $A$ and $B$ have the same average density. Their radii $R_{A}$ and $R_{B}$ are such that $R_{A}: R_{B}=3: 1$. If $g_{A}$ and $g_{B}$ are the acceleration due to gravity at the surfaces of the planets, the $g_{A}: g_{B}$ equals

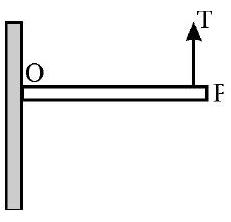
138295 A uniform rod of length of $1 \mathrm{~m}$ and mass of 2 $\mathrm{kg}$ is attached to a side support at $\mathrm{O}$ as shown in the figure. The rod is at equilibrium due to upward force $T$ acting at $P$. Assume the acceleration due to gravity as $10 \mathrm{~m} / \mathrm{s}^{2}$. The value of $T$ is