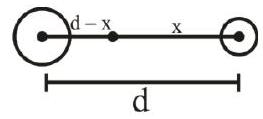
138277 At what distance (in metre) from the centre of the Moon, the intensity of gravitational field will be zero? (Take, mass of Earth and Moon as $5.98 \times 10^{24} \mathrm{~kg}$ and $7.35 \times 10^{22} \mathrm{~kg}$ respectively and the distance between Moon and Earth is $\left.3.85 \times 10^{8} \mathrm{~m}\right)$
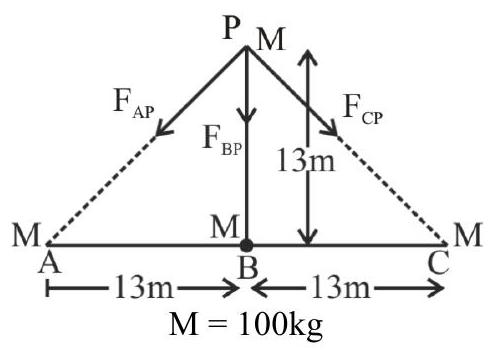
138279 Three identical particle $A, B$ and $C$ of mass 100 $\mathrm{kg}$ each are placed in a straight line with $A B=$ $B C=13 \mathrm{~m}$. The gravitational force on a fourth particle $P$ of the same mass is $F$, when placed at a distance $13 \mathrm{~m}$ from the particle $B$ on the perpendicular bisector of the line AC. The value of $F$ will be approximately:
138277 At what distance (in metre) from the centre of the Moon, the intensity of gravitational field will be zero? (Take, mass of Earth and Moon as $5.98 \times 10^{24} \mathrm{~kg}$ and $7.35 \times 10^{22} \mathrm{~kg}$ respectively and the distance between Moon and Earth is $\left.3.85 \times 10^{8} \mathrm{~m}\right)$
138279 Three identical particle $A, B$ and $C$ of mass 100 $\mathrm{kg}$ each are placed in a straight line with $A B=$ $B C=13 \mathrm{~m}$. The gravitational force on a fourth particle $P$ of the same mass is $F$, when placed at a distance $13 \mathrm{~m}$ from the particle $B$ on the perpendicular bisector of the line AC. The value of $F$ will be approximately:
138277 At what distance (in metre) from the centre of the Moon, the intensity of gravitational field will be zero? (Take, mass of Earth and Moon as $5.98 \times 10^{24} \mathrm{~kg}$ and $7.35 \times 10^{22} \mathrm{~kg}$ respectively and the distance between Moon and Earth is $\left.3.85 \times 10^{8} \mathrm{~m}\right)$
138279 Three identical particle $A, B$ and $C$ of mass 100 $\mathrm{kg}$ each are placed in a straight line with $A B=$ $B C=13 \mathrm{~m}$. The gravitational force on a fourth particle $P$ of the same mass is $F$, when placed at a distance $13 \mathrm{~m}$ from the particle $B$ on the perpendicular bisector of the line AC. The value of $F$ will be approximately:
138277 At what distance (in metre) from the centre of the Moon, the intensity of gravitational field will be zero? (Take, mass of Earth and Moon as $5.98 \times 10^{24} \mathrm{~kg}$ and $7.35 \times 10^{22} \mathrm{~kg}$ respectively and the distance between Moon and Earth is $\left.3.85 \times 10^{8} \mathrm{~m}\right)$
138279 Three identical particle $A, B$ and $C$ of mass 100 $\mathrm{kg}$ each are placed in a straight line with $A B=$ $B C=13 \mathrm{~m}$. The gravitational force on a fourth particle $P$ of the same mass is $F$, when placed at a distance $13 \mathrm{~m}$ from the particle $B$ on the perpendicular bisector of the line AC. The value of $F$ will be approximately:
138277 At what distance (in metre) from the centre of the Moon, the intensity of gravitational field will be zero? (Take, mass of Earth and Moon as $5.98 \times 10^{24} \mathrm{~kg}$ and $7.35 \times 10^{22} \mathrm{~kg}$ respectively and the distance between Moon and Earth is $\left.3.85 \times 10^{8} \mathrm{~m}\right)$
138279 Three identical particle $A, B$ and $C$ of mass 100 $\mathrm{kg}$ each are placed in a straight line with $A B=$ $B C=13 \mathrm{~m}$. The gravitational force on a fourth particle $P$ of the same mass is $F$, when placed at a distance $13 \mathrm{~m}$ from the particle $B$ on the perpendicular bisector of the line AC. The value of $F$ will be approximately: