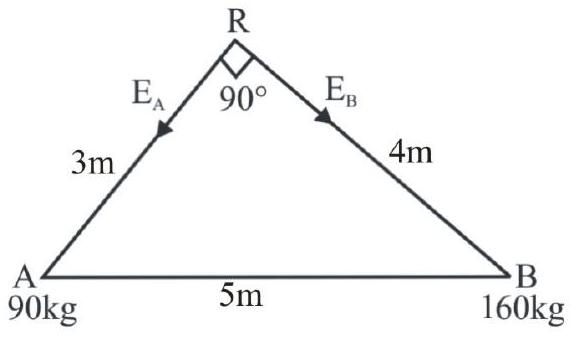
138231 Two masses $90 \mathrm{~kg}$ and $160 \mathrm{~kg}$ are separated by a distance of $5 \mathrm{~m}$. The magnitude of intensity of the gravitational field at a point which is at a distance $3 \mathrm{~m}$ from the $90 \mathrm{~kg}$ mass and $4 \mathrm{~m}$ from the $160 \mathrm{~kg}$ mass is (Universal gravitational constant, $G=6.67 \times 10^{-11} \mathrm{~N}-\mathrm{m}^{2} \mathbf{k g}^{-2}$ ).
138231 Two masses $90 \mathrm{~kg}$ and $160 \mathrm{~kg}$ are separated by a distance of $5 \mathrm{~m}$. The magnitude of intensity of the gravitational field at a point which is at a distance $3 \mathrm{~m}$ from the $90 \mathrm{~kg}$ mass and $4 \mathrm{~m}$ from the $160 \mathrm{~kg}$ mass is (Universal gravitational constant, $G=6.67 \times 10^{-11} \mathrm{~N}-\mathrm{m}^{2} \mathbf{k g}^{-2}$ ).
138231 Two masses $90 \mathrm{~kg}$ and $160 \mathrm{~kg}$ are separated by a distance of $5 \mathrm{~m}$. The magnitude of intensity of the gravitational field at a point which is at a distance $3 \mathrm{~m}$ from the $90 \mathrm{~kg}$ mass and $4 \mathrm{~m}$ from the $160 \mathrm{~kg}$ mass is (Universal gravitational constant, $G=6.67 \times 10^{-11} \mathrm{~N}-\mathrm{m}^{2} \mathbf{k g}^{-2}$ ).
138231 Two masses $90 \mathrm{~kg}$ and $160 \mathrm{~kg}$ are separated by a distance of $5 \mathrm{~m}$. The magnitude of intensity of the gravitational field at a point which is at a distance $3 \mathrm{~m}$ from the $90 \mathrm{~kg}$ mass and $4 \mathrm{~m}$ from the $160 \mathrm{~kg}$ mass is (Universal gravitational constant, $G=6.67 \times 10^{-11} \mathrm{~N}-\mathrm{m}^{2} \mathbf{k g}^{-2}$ ).
138231 Two masses $90 \mathrm{~kg}$ and $160 \mathrm{~kg}$ are separated by a distance of $5 \mathrm{~m}$. The magnitude of intensity of the gravitational field at a point which is at a distance $3 \mathrm{~m}$ from the $90 \mathrm{~kg}$ mass and $4 \mathrm{~m}$ from the $160 \mathrm{~kg}$ mass is (Universal gravitational constant, $G=6.67 \times 10^{-11} \mathrm{~N}-\mathrm{m}^{2} \mathbf{k g}^{-2}$ ).