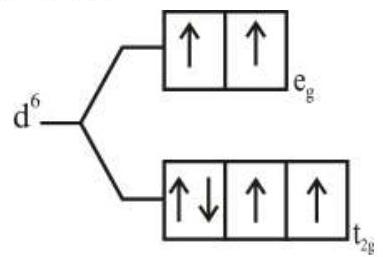
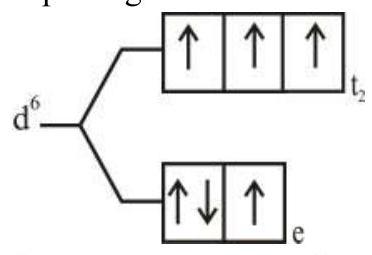
274284 $[\operatorname{Pd}(\mathrm{F})(\mathrm{Cl})(\mathrm{Br})(\mathrm{I})]^{2-}$ has $\mathrm{n}$ number of geometrical isomers. Then, the spin-only magnetic moment and crystal field stabilization energy $[\mathrm{CFSE}]$ of $\left[\mathrm{Fe}(\mathrm{CN})_{6}\right]^{\mathrm{n}-6}$ respectively, are [Note-Ignore the pairing energy]
274284 $[\operatorname{Pd}(\mathrm{F})(\mathrm{Cl})(\mathrm{Br})(\mathrm{I})]^{2-}$ has $\mathrm{n}$ number of geometrical isomers. Then, the spin-only magnetic moment and crystal field stabilization energy $[\mathrm{CFSE}]$ of $\left[\mathrm{Fe}(\mathrm{CN})_{6}\right]^{\mathrm{n}-6}$ respectively, are [Note-Ignore the pairing energy]
274284 $[\operatorname{Pd}(\mathrm{F})(\mathrm{Cl})(\mathrm{Br})(\mathrm{I})]^{2-}$ has $\mathrm{n}$ number of geometrical isomers. Then, the spin-only magnetic moment and crystal field stabilization energy $[\mathrm{CFSE}]$ of $\left[\mathrm{Fe}(\mathrm{CN})_{6}\right]^{\mathrm{n}-6}$ respectively, are [Note-Ignore the pairing energy]
274284 $[\operatorname{Pd}(\mathrm{F})(\mathrm{Cl})(\mathrm{Br})(\mathrm{I})]^{2-}$ has $\mathrm{n}$ number of geometrical isomers. Then, the spin-only magnetic moment and crystal field stabilization energy $[\mathrm{CFSE}]$ of $\left[\mathrm{Fe}(\mathrm{CN})_{6}\right]^{\mathrm{n}-6}$ respectively, are [Note-Ignore the pairing energy]