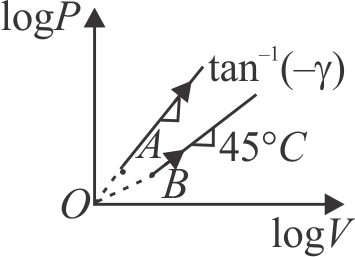371425
Two thermodynamical processes are shown in the figure. The molar heat capacity for process \({A}\) and \({B}\) are \({C_{A}}\) and \({C_{B}}\). The molar heat capacity at constant pressure and constant volume are represented by \({C_{P}}\) and \({C_{V}}\), respectively. Choose the correct statement.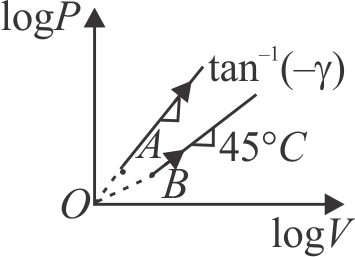
371425
Two thermodynamical processes are shown in the figure. The molar heat capacity for process \({A}\) and \({B}\) are \({C_{A}}\) and \({C_{B}}\). The molar heat capacity at constant pressure and constant volume are represented by \({C_{P}}\) and \({C_{V}}\), respectively. Choose the correct statement.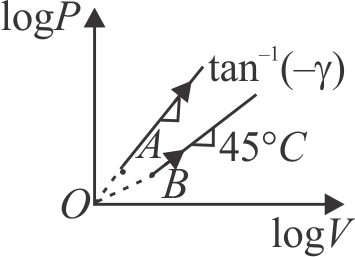
371425
Two thermodynamical processes are shown in the figure. The molar heat capacity for process \({A}\) and \({B}\) are \({C_{A}}\) and \({C_{B}}\). The molar heat capacity at constant pressure and constant volume are represented by \({C_{P}}\) and \({C_{V}}\), respectively. Choose the correct statement.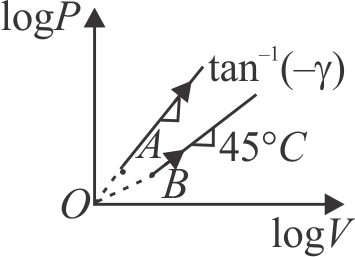
371425
Two thermodynamical processes are shown in the figure. The molar heat capacity for process \({A}\) and \({B}\) are \({C_{A}}\) and \({C_{B}}\). The molar heat capacity at constant pressure and constant volume are represented by \({C_{P}}\) and \({C_{V}}\), respectively. Choose the correct statement.