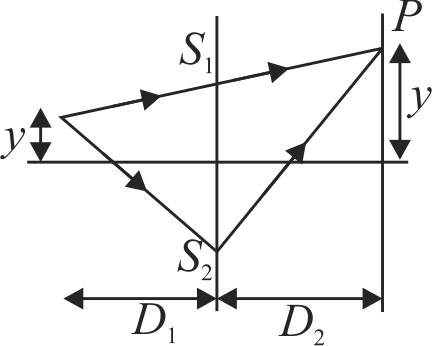
368077 In a Young's double slit experiment set up, source \(S\) of wavelength \(500\;\,nm\) illuminates two slits \(S_{1}\) and \(S_{2}\) which act as two coherent sources. The source \(S\) oscillates about its own position according to the equation \(y=0.5 \sin \pi t\) where \(y\) is in \(mm\) and \(t\) is in seconds. The minimum value of time \(t\) for which the intensity at point \(P\) on the screen exactly infront of the upper slit becomes minimum is: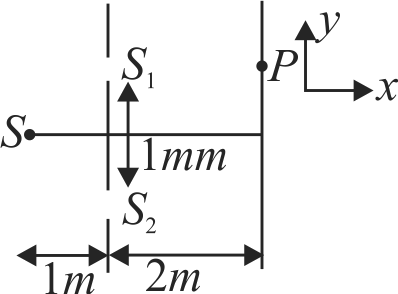

368078 In the Young’s double slit experiment a monochromatic source of wavelength \(\lambda \) is used. The intensity of light passing through each slit Is \({I_0}\) The intensity of light reaching the screen \(SC\) at a point \(P\), a distance \(x\) from \(O\) is given by (Take \(d < < D\) )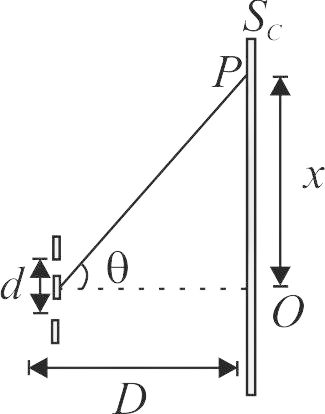

368079 The distance between two coherent sources is \(0.1\,mm\). The fringe-width on a screen \(1.2\,m\) away from the source is \(6.0\,mm\). The wavelength of light used is

368080 In Young's double slit experiment, the wavelength of the light used is doubled and distance between two slits is made half of initial distance. The resultant fringe width becomes

368077 In a Young's double slit experiment set up, source \(S\) of wavelength \(500\;\,nm\) illuminates two slits \(S_{1}\) and \(S_{2}\) which act as two coherent sources. The source \(S\) oscillates about its own position according to the equation \(y=0.5 \sin \pi t\) where \(y\) is in \(mm\) and \(t\) is in seconds. The minimum value of time \(t\) for which the intensity at point \(P\) on the screen exactly infront of the upper slit becomes minimum is:

368078 In the Young’s double slit experiment a monochromatic source of wavelength \(\lambda \) is used. The intensity of light passing through each slit Is \({I_0}\) The intensity of light reaching the screen \(SC\) at a point \(P\), a distance \(x\) from \(O\) is given by (Take \(d < < D\) )

368079 The distance between two coherent sources is \(0.1\,mm\). The fringe-width on a screen \(1.2\,m\) away from the source is \(6.0\,mm\). The wavelength of light used is

368080 In Young's double slit experiment, the wavelength of the light used is doubled and distance between two slits is made half of initial distance. The resultant fringe width becomes

368077 In a Young's double slit experiment set up, source \(S\) of wavelength \(500\;\,nm\) illuminates two slits \(S_{1}\) and \(S_{2}\) which act as two coherent sources. The source \(S\) oscillates about its own position according to the equation \(y=0.5 \sin \pi t\) where \(y\) is in \(mm\) and \(t\) is in seconds. The minimum value of time \(t\) for which the intensity at point \(P\) on the screen exactly infront of the upper slit becomes minimum is:

368078 In the Young’s double slit experiment a monochromatic source of wavelength \(\lambda \) is used. The intensity of light passing through each slit Is \({I_0}\) The intensity of light reaching the screen \(SC\) at a point \(P\), a distance \(x\) from \(O\) is given by (Take \(d < < D\) )

368079 The distance between two coherent sources is \(0.1\,mm\). The fringe-width on a screen \(1.2\,m\) away from the source is \(6.0\,mm\). The wavelength of light used is

368080 In Young's double slit experiment, the wavelength of the light used is doubled and distance between two slits is made half of initial distance. The resultant fringe width becomes

368077 In a Young's double slit experiment set up, source \(S\) of wavelength \(500\;\,nm\) illuminates two slits \(S_{1}\) and \(S_{2}\) which act as two coherent sources. The source \(S\) oscillates about its own position according to the equation \(y=0.5 \sin \pi t\) where \(y\) is in \(mm\) and \(t\) is in seconds. The minimum value of time \(t\) for which the intensity at point \(P\) on the screen exactly infront of the upper slit becomes minimum is:

368078 In the Young’s double slit experiment a monochromatic source of wavelength \(\lambda \) is used. The intensity of light passing through each slit Is \({I_0}\) The intensity of light reaching the screen \(SC\) at a point \(P\), a distance \(x\) from \(O\) is given by (Take \(d < < D\) )

368079 The distance between two coherent sources is \(0.1\,mm\). The fringe-width on a screen \(1.2\,m\) away from the source is \(6.0\,mm\). The wavelength of light used is

368080 In Young's double slit experiment, the wavelength of the light used is doubled and distance between two slits is made half of initial distance. The resultant fringe width becomes