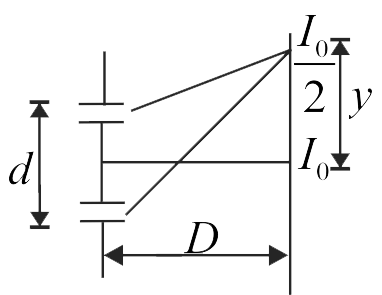
367968 In a biprism experiment, the distance between the slits is \(0.25 {~cm}\) and the distance of screen from slits is \(120 {~cm}\). If the wavelength of light used is \(6000\)\( \mathop A^{~~\circ} \) and \({I}_{0}\) is the intensity of central maximum, then at what distance from the central maxima, the intensity will be \(\dfrac{{I}_{0}}{2}\) ?
367971
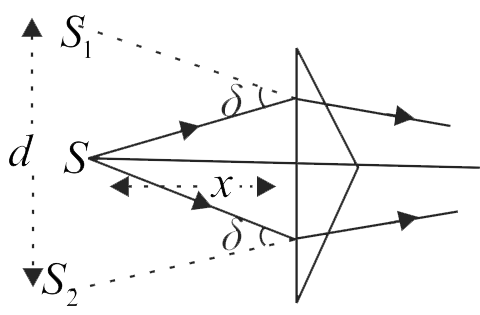
A Fresnel biprism of angle \(2^{\circ}\) is illuminated by light of wavelength \(6280\)\( \mathop A^{~~\circ} \) from a source which is \(0.10 {~m}\) away from it. What will be the width of the fringes formed on a screen kept \(0.9 {~m}\) away from the biprism?
(Take Refractive index of glass \( = 1.5,\pi = 3.14\))
367968 In a biprism experiment, the distance between the slits is \(0.25 {~cm}\) and the distance of screen from slits is \(120 {~cm}\). If the wavelength of light used is \(6000\)\( \mathop A^{~~\circ} \) and \({I}_{0}\) is the intensity of central maximum, then at what distance from the central maxima, the intensity will be \(\dfrac{{I}_{0}}{2}\) ?
367971
A Fresnel biprism of angle \(2^{\circ}\) is illuminated by light of wavelength \(6280\)\( \mathop A^{~~\circ} \) from a source which is \(0.10 {~m}\) away from it. What will be the width of the fringes formed on a screen kept \(0.9 {~m}\) away from the biprism?
(Take Refractive index of glass \( = 1.5,\pi = 3.14\))
367968 In a biprism experiment, the distance between the slits is \(0.25 {~cm}\) and the distance of screen from slits is \(120 {~cm}\). If the wavelength of light used is \(6000\)\( \mathop A^{~~\circ} \) and \({I}_{0}\) is the intensity of central maximum, then at what distance from the central maxima, the intensity will be \(\dfrac{{I}_{0}}{2}\) ?
367971
A Fresnel biprism of angle \(2^{\circ}\) is illuminated by light of wavelength \(6280\)\( \mathop A^{~~\circ} \) from a source which is \(0.10 {~m}\) away from it. What will be the width of the fringes formed on a screen kept \(0.9 {~m}\) away from the biprism?
(Take Refractive index of glass \( = 1.5,\pi = 3.14\))
367968 In a biprism experiment, the distance between the slits is \(0.25 {~cm}\) and the distance of screen from slits is \(120 {~cm}\). If the wavelength of light used is \(6000\)\( \mathop A^{~~\circ} \) and \({I}_{0}\) is the intensity of central maximum, then at what distance from the central maxima, the intensity will be \(\dfrac{{I}_{0}}{2}\) ?
367971
A Fresnel biprism of angle \(2^{\circ}\) is illuminated by light of wavelength \(6280\)\( \mathop A^{~~\circ} \) from a source which is \(0.10 {~m}\) away from it. What will be the width of the fringes formed on a screen kept \(0.9 {~m}\) away from the biprism?
(Take Refractive index of glass \( = 1.5,\pi = 3.14\))
367968 In a biprism experiment, the distance between the slits is \(0.25 {~cm}\) and the distance of screen from slits is \(120 {~cm}\). If the wavelength of light used is \(6000\)\( \mathop A^{~~\circ} \) and \({I}_{0}\) is the intensity of central maximum, then at what distance from the central maxima, the intensity will be \(\dfrac{{I}_{0}}{2}\) ?
367971
A Fresnel biprism of angle \(2^{\circ}\) is illuminated by light of wavelength \(6280\)\( \mathop A^{~~\circ} \) from a source which is \(0.10 {~m}\) away from it. What will be the width of the fringes formed on a screen kept \(0.9 {~m}\) away from the biprism?
(Take Refractive index of glass \( = 1.5,\pi = 3.14\))