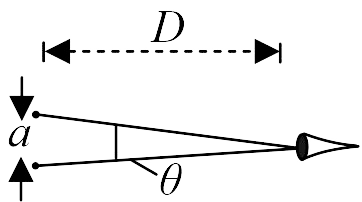
367908 The head lights of a jeep are 1.2 \(m\) apart. If the pupil of the eye of an observer has a diameter of 2 \(mm\) and light of wavelength \(5896\mathop A\limits^ \circ \) is used, what should be the maximum distance of the jeep from the observer if the two head lights are just separated ?
367910 Two luminous point sources separated by a certain distance are at 10 \(km\) form an observe. If the aperture of his eye is \(2.5 \times {10^{ - 3}}\;m\) and the wavelength of light used is 500\(nm\), the distance of separation between the point sources just seen to be resolved is
367908 The head lights of a jeep are 1.2 \(m\) apart. If the pupil of the eye of an observer has a diameter of 2 \(mm\) and light of wavelength \(5896\mathop A\limits^ \circ \) is used, what should be the maximum distance of the jeep from the observer if the two head lights are just separated ?
367910 Two luminous point sources separated by a certain distance are at 10 \(km\) form an observe. If the aperture of his eye is \(2.5 \times {10^{ - 3}}\;m\) and the wavelength of light used is 500\(nm\), the distance of separation between the point sources just seen to be resolved is
367908 The head lights of a jeep are 1.2 \(m\) apart. If the pupil of the eye of an observer has a diameter of 2 \(mm\) and light of wavelength \(5896\mathop A\limits^ \circ \) is used, what should be the maximum distance of the jeep from the observer if the two head lights are just separated ?
367910 Two luminous point sources separated by a certain distance are at 10 \(km\) form an observe. If the aperture of his eye is \(2.5 \times {10^{ - 3}}\;m\) and the wavelength of light used is 500\(nm\), the distance of separation between the point sources just seen to be resolved is
367908 The head lights of a jeep are 1.2 \(m\) apart. If the pupil of the eye of an observer has a diameter of 2 \(mm\) and light of wavelength \(5896\mathop A\limits^ \circ \) is used, what should be the maximum distance of the jeep from the observer if the two head lights are just separated ?
367910 Two luminous point sources separated by a certain distance are at 10 \(km\) form an observe. If the aperture of his eye is \(2.5 \times {10^{ - 3}}\;m\) and the wavelength of light used is 500\(nm\), the distance of separation between the point sources just seen to be resolved is
367908 The head lights of a jeep are 1.2 \(m\) apart. If the pupil of the eye of an observer has a diameter of 2 \(mm\) and light of wavelength \(5896\mathop A\limits^ \circ \) is used, what should be the maximum distance of the jeep from the observer if the two head lights are just separated ?
367910 Two luminous point sources separated by a certain distance are at 10 \(km\) form an observe. If the aperture of his eye is \(2.5 \times {10^{ - 3}}\;m\) and the wavelength of light used is 500\(nm\), the distance of separation between the point sources just seen to be resolved is