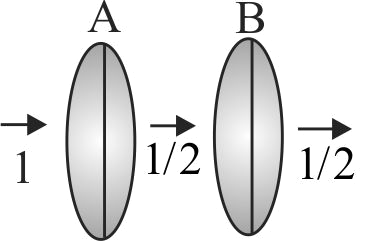
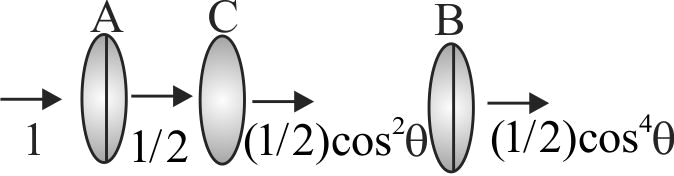367855 Unpolarized light of intensity \(I\) passes through an ideal polarizer \(A\). Another identical polarizer \(B\) is placed behind \(A\). The intensity of light beyond \(B\) is found to be \(\frac{1}{2}\). Now another identical polarizer \(C\) is placed between \(A\) and \(B\). The intensity beyond \(B\) is now found to be \(\frac{1}{8}\). The angle between polarizer \(A\) and \(B\) is:
367858 Two beams, \(A\) and \(B\), of plane polarised light with mutually perpendicular planes of polarisation are seen through a polaroid. From the position when the beam \(A\) has maximum intensity (and beam \(B\) has zero intensity), a rotation of Polaroid through \(30^\circ \) makes the two beams appear equally bright. If the initial intensities of the two beams are \({I_A}\) and \({I_B}\) respectively, then \({I_A}{\rm{/ }}{I_B}\) equals:
367855 Unpolarized light of intensity \(I\) passes through an ideal polarizer \(A\). Another identical polarizer \(B\) is placed behind \(A\). The intensity of light beyond \(B\) is found to be \(\frac{1}{2}\). Now another identical polarizer \(C\) is placed between \(A\) and \(B\). The intensity beyond \(B\) is now found to be \(\frac{1}{8}\). The angle between polarizer \(A\) and \(B\) is:
367858 Two beams, \(A\) and \(B\), of plane polarised light with mutually perpendicular planes of polarisation are seen through a polaroid. From the position when the beam \(A\) has maximum intensity (and beam \(B\) has zero intensity), a rotation of Polaroid through \(30^\circ \) makes the two beams appear equally bright. If the initial intensities of the two beams are \({I_A}\) and \({I_B}\) respectively, then \({I_A}{\rm{/ }}{I_B}\) equals:
367855 Unpolarized light of intensity \(I\) passes through an ideal polarizer \(A\). Another identical polarizer \(B\) is placed behind \(A\). The intensity of light beyond \(B\) is found to be \(\frac{1}{2}\). Now another identical polarizer \(C\) is placed between \(A\) and \(B\). The intensity beyond \(B\) is now found to be \(\frac{1}{8}\). The angle between polarizer \(A\) and \(B\) is:
367858 Two beams, \(A\) and \(B\), of plane polarised light with mutually perpendicular planes of polarisation are seen through a polaroid. From the position when the beam \(A\) has maximum intensity (and beam \(B\) has zero intensity), a rotation of Polaroid through \(30^\circ \) makes the two beams appear equally bright. If the initial intensities of the two beams are \({I_A}\) and \({I_B}\) respectively, then \({I_A}{\rm{/ }}{I_B}\) equals:
367855 Unpolarized light of intensity \(I\) passes through an ideal polarizer \(A\). Another identical polarizer \(B\) is placed behind \(A\). The intensity of light beyond \(B\) is found to be \(\frac{1}{2}\). Now another identical polarizer \(C\) is placed between \(A\) and \(B\). The intensity beyond \(B\) is now found to be \(\frac{1}{8}\). The angle between polarizer \(A\) and \(B\) is:
367858 Two beams, \(A\) and \(B\), of plane polarised light with mutually perpendicular planes of polarisation are seen through a polaroid. From the position when the beam \(A\) has maximum intensity (and beam \(B\) has zero intensity), a rotation of Polaroid through \(30^\circ \) makes the two beams appear equally bright. If the initial intensities of the two beams are \({I_A}\) and \({I_B}\) respectively, then \({I_A}{\rm{/ }}{I_B}\) equals:
367855 Unpolarized light of intensity \(I\) passes through an ideal polarizer \(A\). Another identical polarizer \(B\) is placed behind \(A\). The intensity of light beyond \(B\) is found to be \(\frac{1}{2}\). Now another identical polarizer \(C\) is placed between \(A\) and \(B\). The intensity beyond \(B\) is now found to be \(\frac{1}{8}\). The angle between polarizer \(A\) and \(B\) is:
367858 Two beams, \(A\) and \(B\), of plane polarised light with mutually perpendicular planes of polarisation are seen through a polaroid. From the position when the beam \(A\) has maximum intensity (and beam \(B\) has zero intensity), a rotation of Polaroid through \(30^\circ \) makes the two beams appear equally bright. If the initial intensities of the two beams are \({I_A}\) and \({I_B}\) respectively, then \({I_A}{\rm{/ }}{I_B}\) equals: