367791
A monochromatic light source of wavelength \(\lambda\) is placed at \(S\). Three slits \(S_{1}, S_{2}\) and \(S_{3}\) are equidistant from the source \(S\) and the point \(P\) on the screen. \(S_{1} P-S_{2} P=\lambda / 6\) and \(S_{1} P-S_{3} P=2 \lambda / 3\). If \(I\) be the intensity at \(P\) when only one slit \(S_{3}\) is open, the intensity at \(P\) when all the three slits are open is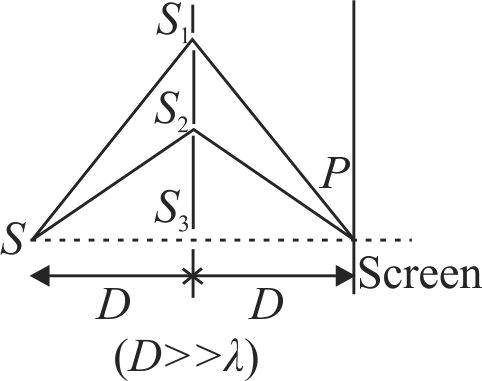
367791
A monochromatic light source of wavelength \(\lambda\) is placed at \(S\). Three slits \(S_{1}, S_{2}\) and \(S_{3}\) are equidistant from the source \(S\) and the point \(P\) on the screen. \(S_{1} P-S_{2} P=\lambda / 6\) and \(S_{1} P-S_{3} P=2 \lambda / 3\). If \(I\) be the intensity at \(P\) when only one slit \(S_{3}\) is open, the intensity at \(P\) when all the three slits are open is
367791
A monochromatic light source of wavelength \(\lambda\) is placed at \(S\). Three slits \(S_{1}, S_{2}\) and \(S_{3}\) are equidistant from the source \(S\) and the point \(P\) on the screen. \(S_{1} P-S_{2} P=\lambda / 6\) and \(S_{1} P-S_{3} P=2 \lambda / 3\). If \(I\) be the intensity at \(P\) when only one slit \(S_{3}\) is open, the intensity at \(P\) when all the three slits are open is
367791
A monochromatic light source of wavelength \(\lambda\) is placed at \(S\). Three slits \(S_{1}, S_{2}\) and \(S_{3}\) are equidistant from the source \(S\) and the point \(P\) on the screen. \(S_{1} P-S_{2} P=\lambda / 6\) and \(S_{1} P-S_{3} P=2 \lambda / 3\). If \(I\) be the intensity at \(P\) when only one slit \(S_{3}\) is open, the intensity at \(P\) when all the three slits are open is

