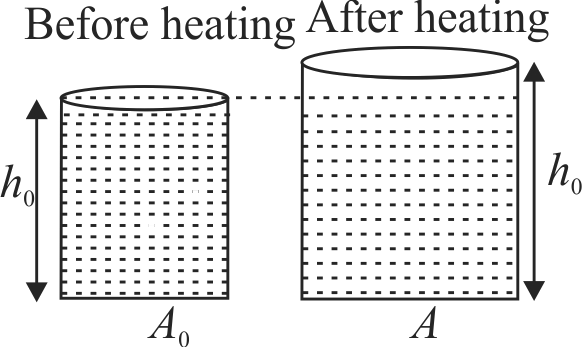
366717
The figure shows a glass cylinder (linear coefficient of expansion is \(\alpha\) ) completely filled with a liquid of volume expansion co-efficient \(\gamma\). On heating length of the liquid column does not change. Choose the correct relation between \(\gamma\) and \(\alpha\)
366718 A glass flask is filled up to a mark with \(50\,cc\) of mercury at \(18^\circ C\). If the flask and contents are heated to \(38^\circ C\), how much mercury will be above the mark ( \(\alpha\) for glass is \(9 \times {10^{ - 6}}/^\circ C\) and coefficient of real expansion of mercury is \(180 \times {10^{ - 6}}/^\circ C\) )
366719 The coefficient of apparent expansion of mercury in a glass vessel is \(153 \times {10^{ - 6}}/^\circ C\) and in a steel vessel is \(144 \times {10^{ - 6}}/^\circ C\). If \(\alpha\) for steel is \(12 \times {10^{ - 6}}/^\circ C\), then \(\alpha\) that of glass is :
366717
The figure shows a glass cylinder (linear coefficient of expansion is \(\alpha\) ) completely filled with a liquid of volume expansion co-efficient \(\gamma\). On heating length of the liquid column does not change. Choose the correct relation between \(\gamma\) and \(\alpha\)
366718 A glass flask is filled up to a mark with \(50\,cc\) of mercury at \(18^\circ C\). If the flask and contents are heated to \(38^\circ C\), how much mercury will be above the mark ( \(\alpha\) for glass is \(9 \times {10^{ - 6}}/^\circ C\) and coefficient of real expansion of mercury is \(180 \times {10^{ - 6}}/^\circ C\) )
366719 The coefficient of apparent expansion of mercury in a glass vessel is \(153 \times {10^{ - 6}}/^\circ C\) and in a steel vessel is \(144 \times {10^{ - 6}}/^\circ C\). If \(\alpha\) for steel is \(12 \times {10^{ - 6}}/^\circ C\), then \(\alpha\) that of glass is :
366717
The figure shows a glass cylinder (linear coefficient of expansion is \(\alpha\) ) completely filled with a liquid of volume expansion co-efficient \(\gamma\). On heating length of the liquid column does not change. Choose the correct relation between \(\gamma\) and \(\alpha\)
366718 A glass flask is filled up to a mark with \(50\,cc\) of mercury at \(18^\circ C\). If the flask and contents are heated to \(38^\circ C\), how much mercury will be above the mark ( \(\alpha\) for glass is \(9 \times {10^{ - 6}}/^\circ C\) and coefficient of real expansion of mercury is \(180 \times {10^{ - 6}}/^\circ C\) )
366719 The coefficient of apparent expansion of mercury in a glass vessel is \(153 \times {10^{ - 6}}/^\circ C\) and in a steel vessel is \(144 \times {10^{ - 6}}/^\circ C\). If \(\alpha\) for steel is \(12 \times {10^{ - 6}}/^\circ C\), then \(\alpha\) that of glass is :
366717
The figure shows a glass cylinder (linear coefficient of expansion is \(\alpha\) ) completely filled with a liquid of volume expansion co-efficient \(\gamma\). On heating length of the liquid column does not change. Choose the correct relation between \(\gamma\) and \(\alpha\)
366718 A glass flask is filled up to a mark with \(50\,cc\) of mercury at \(18^\circ C\). If the flask and contents are heated to \(38^\circ C\), how much mercury will be above the mark ( \(\alpha\) for glass is \(9 \times {10^{ - 6}}/^\circ C\) and coefficient of real expansion of mercury is \(180 \times {10^{ - 6}}/^\circ C\) )
366719 The coefficient of apparent expansion of mercury in a glass vessel is \(153 \times {10^{ - 6}}/^\circ C\) and in a steel vessel is \(144 \times {10^{ - 6}}/^\circ C\). If \(\alpha\) for steel is \(12 \times {10^{ - 6}}/^\circ C\), then \(\alpha\) that of glass is :
366717
The figure shows a glass cylinder (linear coefficient of expansion is \(\alpha\) ) completely filled with a liquid of volume expansion co-efficient \(\gamma\). On heating length of the liquid column does not change. Choose the correct relation between \(\gamma\) and \(\alpha\)
366718 A glass flask is filled up to a mark with \(50\,cc\) of mercury at \(18^\circ C\). If the flask and contents are heated to \(38^\circ C\), how much mercury will be above the mark ( \(\alpha\) for glass is \(9 \times {10^{ - 6}}/^\circ C\) and coefficient of real expansion of mercury is \(180 \times {10^{ - 6}}/^\circ C\) )
366719 The coefficient of apparent expansion of mercury in a glass vessel is \(153 \times {10^{ - 6}}/^\circ C\) and in a steel vessel is \(144 \times {10^{ - 6}}/^\circ C\). If \(\alpha\) for steel is \(12 \times {10^{ - 6}}/^\circ C\), then \(\alpha\) that of glass is :