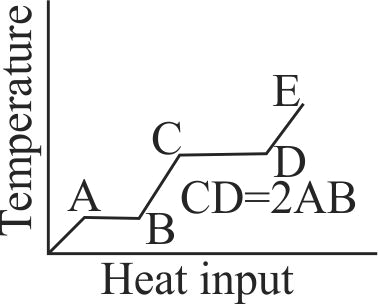
366330 A solid cube of mass \({m}\) at a temperature \({\theta_{0}}\) is heated at a constant rate. It becomes liquid at temperature \({\theta_{1}}\) and vapour at temperature \({\theta_{2}}\). Let \({s_{1}}\) and \({s_{2}}\) be specific heats in its solid and liquid states respectively. If \({L_{f}}\) and \({L_{v}}\) are latent heats of fusion and vaporisation respectively, then the minimum heat energy supplied to the cube until it vaporises is
366330 A solid cube of mass \({m}\) at a temperature \({\theta_{0}}\) is heated at a constant rate. It becomes liquid at temperature \({\theta_{1}}\) and vapour at temperature \({\theta_{2}}\). Let \({s_{1}}\) and \({s_{2}}\) be specific heats in its solid and liquid states respectively. If \({L_{f}}\) and \({L_{v}}\) are latent heats of fusion and vaporisation respectively, then the minimum heat energy supplied to the cube until it vaporises is
366330 A solid cube of mass \({m}\) at a temperature \({\theta_{0}}\) is heated at a constant rate. It becomes liquid at temperature \({\theta_{1}}\) and vapour at temperature \({\theta_{2}}\). Let \({s_{1}}\) and \({s_{2}}\) be specific heats in its solid and liquid states respectively. If \({L_{f}}\) and \({L_{v}}\) are latent heats of fusion and vaporisation respectively, then the minimum heat energy supplied to the cube until it vaporises is
366330 A solid cube of mass \({m}\) at a temperature \({\theta_{0}}\) is heated at a constant rate. It becomes liquid at temperature \({\theta_{1}}\) and vapour at temperature \({\theta_{2}}\). Let \({s_{1}}\) and \({s_{2}}\) be specific heats in its solid and liquid states respectively. If \({L_{f}}\) and \({L_{v}}\) are latent heats of fusion and vaporisation respectively, then the minimum heat energy supplied to the cube until it vaporises is