363337
Three blocks \({m_{1}, m_{2}}\), and \({m_{3}}\) of masses \({1.5 {~kg}, 2.0 {~kg}}\), and \(10\,kg,\) respectively, are placed on a rough surface \({(\mu=0.20)}\), as shown in the figure. If a force \({F}\) is applied to give blocks an acceleration of \({3.0 {~m} / {s}^{2}}\), then the force that the \(1.50\,kg\) block exerts on the \(2.0\,kg\) block will be approximately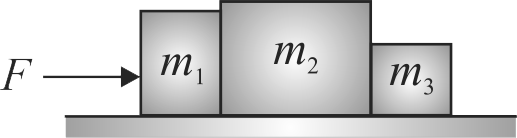
363338
A 10 \(kg\) block is resting on the horizontal surface when the force \(F\) is applied to it for 7 sec. The variation of \(F\) with time is shown in the figure. The coefficients of static and kinetic friction both are equal to 0.50. Find velocity of the block (in \(m\)/\(s\)) at \(t = 4\sec \).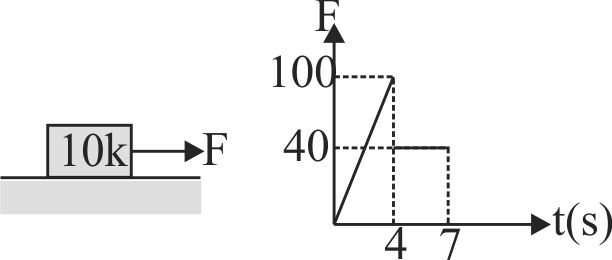
363337
Three blocks \({m_{1}, m_{2}}\), and \({m_{3}}\) of masses \({1.5 {~kg}, 2.0 {~kg}}\), and \(10\,kg,\) respectively, are placed on a rough surface \({(\mu=0.20)}\), as shown in the figure. If a force \({F}\) is applied to give blocks an acceleration of \({3.0 {~m} / {s}^{2}}\), then the force that the \(1.50\,kg\) block exerts on the \(2.0\,kg\) block will be approximately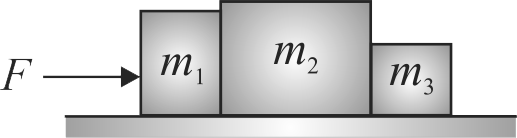
363338
A 10 \(kg\) block is resting on the horizontal surface when the force \(F\) is applied to it for 7 sec. The variation of \(F\) with time is shown in the figure. The coefficients of static and kinetic friction both are equal to 0.50. Find velocity of the block (in \(m\)/\(s\)) at \(t = 4\sec \).
363337
Three blocks \({m_{1}, m_{2}}\), and \({m_{3}}\) of masses \({1.5 {~kg}, 2.0 {~kg}}\), and \(10\,kg,\) respectively, are placed on a rough surface \({(\mu=0.20)}\), as shown in the figure. If a force \({F}\) is applied to give blocks an acceleration of \({3.0 {~m} / {s}^{2}}\), then the force that the \(1.50\,kg\) block exerts on the \(2.0\,kg\) block will be approximately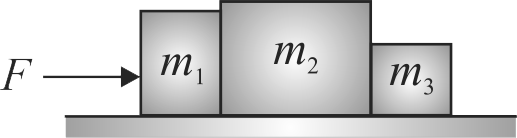
363338
A 10 \(kg\) block is resting on the horizontal surface when the force \(F\) is applied to it for 7 sec. The variation of \(F\) with time is shown in the figure. The coefficients of static and kinetic friction both are equal to 0.50. Find velocity of the block (in \(m\)/\(s\)) at \(t = 4\sec \).
363337
Three blocks \({m_{1}, m_{2}}\), and \({m_{3}}\) of masses \({1.5 {~kg}, 2.0 {~kg}}\), and \(10\,kg,\) respectively, are placed on a rough surface \({(\mu=0.20)}\), as shown in the figure. If a force \({F}\) is applied to give blocks an acceleration of \({3.0 {~m} / {s}^{2}}\), then the force that the \(1.50\,kg\) block exerts on the \(2.0\,kg\) block will be approximately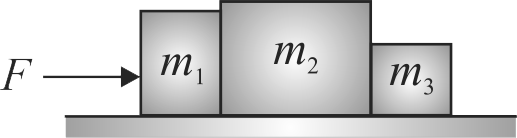
363338
A 10 \(kg\) block is resting on the horizontal surface when the force \(F\) is applied to it for 7 sec. The variation of \(F\) with time is shown in the figure. The coefficients of static and kinetic friction both are equal to 0.50. Find velocity of the block (in \(m\)/\(s\)) at \(t = 4\sec \).
