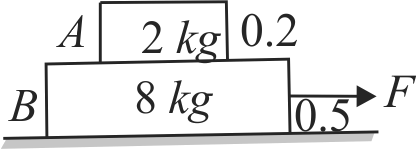363322 A stationary body of mass \({m}\) is slowly lowered onto a massive platform of mass \({M(M>>m)}\) moving at a speed \({v_{0}=4 {~m} / {s}}\). How much will the body slide (in \(m\)) with respect to the platform \({\left(\mu=0.2\right.}\) and \({\left.g=10 {~m} / {s}^{2}\right)}\)?

363323 A 40 \(kg\) slab rests on a frictionless floor. A 10 \(kg\) block rests on top of the slab. The static coefficient of friction between the block and the slab is 0.60 while the kinetic coefficient of friction is 0.40. The 10 \(kg\) block is acted upon by a horizontal force of 100 \(N\). The resulting acceleration of the slab will be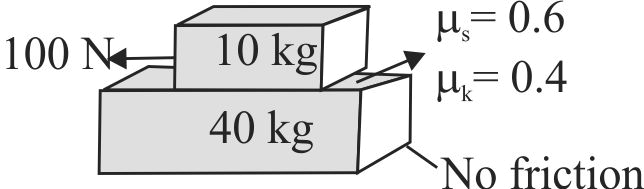

363324 Block \(A\) of mass 2 \(kg\) is placed over a block \(B\) of mass 8 \(kg\). The combination is placed on a rough horizontal surface. If \(g = 10\,m{s^{ - 2}},\) coefficient of friction between \(B\) and floor \( = 0.5\), coefficient of friction between \(A\) and \(B = 0.4\) and a horizontal force of 10 \(N\) is applied on 8 \(kg\) block, then the force of friction between \(A\) and \(B\) is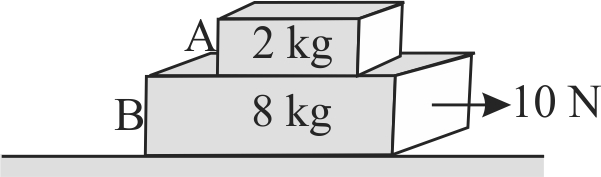

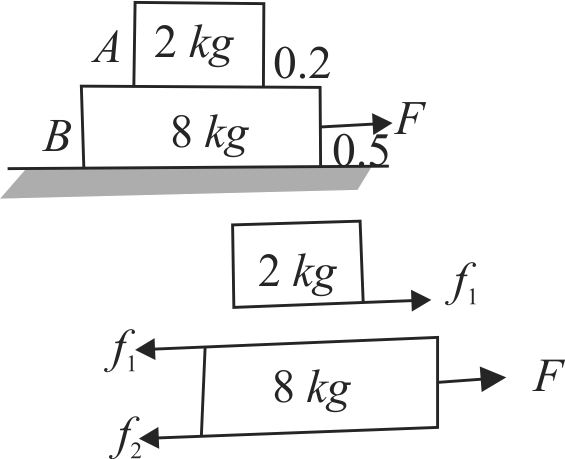
363325 A block \(A\) of mass 2 \(kg\) rests on another block \(B\) of mass 8 \(kg\) which rests on a horizontal floor. The coefficient of friction between \(A\) and \(B\) is 0.2 while that between \(B\) and floor is 0.5. When a horizontal force of 25 \(N\) is applied on the block \(B\), find the force of friction between \(A\) and \(B\) \({\rm{(in}}\,\,N{\rm{)}}\) Take \(g=10 {~m} / {s}^{2}\) ).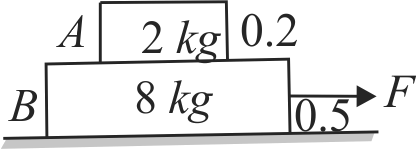

363322 A stationary body of mass \({m}\) is slowly lowered onto a massive platform of mass \({M(M>>m)}\) moving at a speed \({v_{0}=4 {~m} / {s}}\). How much will the body slide (in \(m\)) with respect to the platform \({\left(\mu=0.2\right.}\) and \({\left.g=10 {~m} / {s}^{2}\right)}\)?

363323 A 40 \(kg\) slab rests on a frictionless floor. A 10 \(kg\) block rests on top of the slab. The static coefficient of friction between the block and the slab is 0.60 while the kinetic coefficient of friction is 0.40. The 10 \(kg\) block is acted upon by a horizontal force of 100 \(N\). The resulting acceleration of the slab will be

363324 Block \(A\) of mass 2 \(kg\) is placed over a block \(B\) of mass 8 \(kg\). The combination is placed on a rough horizontal surface. If \(g = 10\,m{s^{ - 2}},\) coefficient of friction between \(B\) and floor \( = 0.5\), coefficient of friction between \(A\) and \(B = 0.4\) and a horizontal force of 10 \(N\) is applied on 8 \(kg\) block, then the force of friction between \(A\) and \(B\) is

363325 A block \(A\) of mass 2 \(kg\) rests on another block \(B\) of mass 8 \(kg\) which rests on a horizontal floor. The coefficient of friction between \(A\) and \(B\) is 0.2 while that between \(B\) and floor is 0.5. When a horizontal force of 25 \(N\) is applied on the block \(B\), find the force of friction between \(A\) and \(B\) \({\rm{(in}}\,\,N{\rm{)}}\) Take \(g=10 {~m} / {s}^{2}\) ).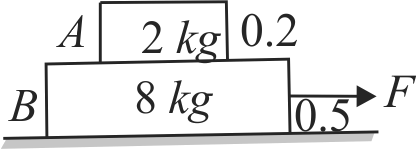

363322 A stationary body of mass \({m}\) is slowly lowered onto a massive platform of mass \({M(M>>m)}\) moving at a speed \({v_{0}=4 {~m} / {s}}\). How much will the body slide (in \(m\)) with respect to the platform \({\left(\mu=0.2\right.}\) and \({\left.g=10 {~m} / {s}^{2}\right)}\)?

363323 A 40 \(kg\) slab rests on a frictionless floor. A 10 \(kg\) block rests on top of the slab. The static coefficient of friction between the block and the slab is 0.60 while the kinetic coefficient of friction is 0.40. The 10 \(kg\) block is acted upon by a horizontal force of 100 \(N\). The resulting acceleration of the slab will be

363324 Block \(A\) of mass 2 \(kg\) is placed over a block \(B\) of mass 8 \(kg\). The combination is placed on a rough horizontal surface. If \(g = 10\,m{s^{ - 2}},\) coefficient of friction between \(B\) and floor \( = 0.5\), coefficient of friction between \(A\) and \(B = 0.4\) and a horizontal force of 10 \(N\) is applied on 8 \(kg\) block, then the force of friction between \(A\) and \(B\) is

363325 A block \(A\) of mass 2 \(kg\) rests on another block \(B\) of mass 8 \(kg\) which rests on a horizontal floor. The coefficient of friction between \(A\) and \(B\) is 0.2 while that between \(B\) and floor is 0.5. When a horizontal force of 25 \(N\) is applied on the block \(B\), find the force of friction between \(A\) and \(B\) \({\rm{(in}}\,\,N{\rm{)}}\) Take \(g=10 {~m} / {s}^{2}\) ).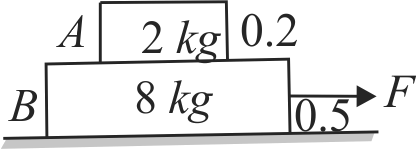

363322 A stationary body of mass \({m}\) is slowly lowered onto a massive platform of mass \({M(M>>m)}\) moving at a speed \({v_{0}=4 {~m} / {s}}\). How much will the body slide (in \(m\)) with respect to the platform \({\left(\mu=0.2\right.}\) and \({\left.g=10 {~m} / {s}^{2}\right)}\)?

363323 A 40 \(kg\) slab rests on a frictionless floor. A 10 \(kg\) block rests on top of the slab. The static coefficient of friction between the block and the slab is 0.60 while the kinetic coefficient of friction is 0.40. The 10 \(kg\) block is acted upon by a horizontal force of 100 \(N\). The resulting acceleration of the slab will be

363324 Block \(A\) of mass 2 \(kg\) is placed over a block \(B\) of mass 8 \(kg\). The combination is placed on a rough horizontal surface. If \(g = 10\,m{s^{ - 2}},\) coefficient of friction between \(B\) and floor \( = 0.5\), coefficient of friction between \(A\) and \(B = 0.4\) and a horizontal force of 10 \(N\) is applied on 8 \(kg\) block, then the force of friction between \(A\) and \(B\) is

363325 A block \(A\) of mass 2 \(kg\) rests on another block \(B\) of mass 8 \(kg\) which rests on a horizontal floor. The coefficient of friction between \(A\) and \(B\) is 0.2 while that between \(B\) and floor is 0.5. When a horizontal force of 25 \(N\) is applied on the block \(B\), find the force of friction between \(A\) and \(B\) \({\rm{(in}}\,\,N{\rm{)}}\) Take \(g=10 {~m} / {s}^{2}\) ).